Advertisements
Advertisements
प्रश्न
विमाओं 50 m × 40 m वाले एक आयताकार लॉन के बीचो-बीच में एक आयताकार तालाब इस प्रकार बनाया जाना है कि तालाब के चारों ओर लगी घास वाले भाग का क्षेत्रफल 1184 m2 हो [आंकड़ा देखें]। तालाब की लंबाई और चौड़ाई ज्ञात कीजिए।

उत्तर
दिया गया है कि विमाओं 50 m × 40 m के एक आयताकार लॉन के केंद्र में एक आयताकार तालाब का निर्माण करना है।
तो, तालाब के चारों ओर तालाब और लॉन के बीच की दूरी समान होगी।
कहो x m
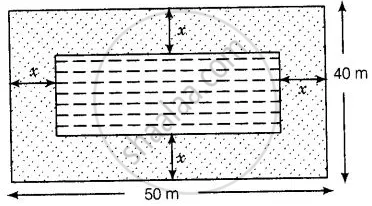
अब, आयताकार लॉन की लंबाई (l1) = 50 m और आयताकार लॉन की चौड़ाई (b1) = 40 m
आयताकार तालाब की लंबाई (l2)= 50 – (x + x) = 50 – 2x
और आयताकार तालाब की चौड़ाई (b2) = 40 – (x + x) = 40 – 2x
साथ ही, तालाब के चारों ओर घास का क्षेत्रफल = 1184 m2
आयताकार लॉन का क्षेत्रफल – आयताकार तालाब का क्षेत्रफल = तालाब के चारों ओर घास का क्षेत्रफल
l1 × b1 – l2 × b2 = 1184 ......[∵ आयत का क्षेत्रफल = लंबाई × चौड़ाई]
⇒ 50 × 40 – (50 – 2x)(40 – 2x) = 1184
⇒ 2000 – (2000 – 80x – 100x + 4x2) = 1184
⇒ 80x + 100x – 4x2 = 1184
⇒ 4x2 – 180x + 1184 = 0
⇒ x2 – 45x + 296 = 0
⇒ x2 – 37x – 8x + 296 = 0 ....[मध्य पद को विभाजित करके]
⇒ x(x – 37) – 8(x – 37) = 0
⇒ (x – 37)(x – 8) = 0
∴ x = 8
x = 37 पर,
तालाब की लंबाई और चौड़ाई क्रमशः – 24 और – 34 है, लेकिन लंबाई और चौड़ाई ऋणात्मक नहीं हो सकती।
तो, x = 37 संभव नहीं हो सकता।
∴ तालाब की लंबाई = 50 – 2x
= 50 – 2(8)
= 50 – 16
= 34 m
और तालाब की चौड़ाई = 40 – 2x
= 40 – 2(8)
= 40 – 16
= 24 m
अतः, तालाब की आवश्यक लंबाई और चौड़ाई क्रमशः 34 m और 24 m है।
APPEARS IN
संबंधित प्रश्न
यदि निम्नलिखित द्विघात समीकरण के मूल का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए:
`4x^2 + 4sqrt3x + 3 = 0`
यदि निम्नलिखित द्विघात समीकरण के मूल का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए:
2x2 + x + 4 = 0
नीचे दिए गए प्रश्न को द्विघात समीकरण के मूल, द्विघात सूत्र का उपयोग करके, ज्ञात कीजिए।
2x2 - 7x + 3 = 0
नीचे दिए गए प्रश्न को द्विघात समीकरण के मूल, द्विघात सूत्र का उपयोग करके, ज्ञात कीजिए।
2x2 + x - 4 = 0
नीचे दिए गए प्रश्न को द्विघात समीकरण के मूल, द्विघात सूत्र का उपयोग करके, ज्ञात कीजिए।
`4x^2 + 4sqrt3x + 3 = 0`
नीचे दिए गए प्रश्न को द्विघात समीकरण के मूल, द्विघात सूत्र का उपयोग करके, ज्ञात कीजिए।
2x2 + x + 4 = 0
दो संख्याओं के वर्गों का अंतर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का आठ गुना है। दोनों संख्याएँ ज्ञात कीजिए।
एक रेलगाड़ी एक समान चाल से 360 km की दूरी तय करती है। यदि यह चाल 5 km/h अधिक होती, तो वह उसी यात्रा में 1 घंटा कम समय लेती। रेलगाड़ी की चाल ज्ञात कीजिए।
दो वर्गों के क्षेत्रफलों का योग 468 m2 है। यदि उनके परिमापों का अंतर 24 m हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
यह ज्ञात हुआ है कि सायं 2 बजकर t मिनट पर किसी घड़ी की मिनट वाली सुई को सायं 3 बजे का समय दर्शाने के लिए `t^2/4` मिनट से 3 मिनट कम समय की आवश्यकता है। t ज्ञात कीजिए।
