Advertisements
Advertisements
Question
विमाओं 50 m × 40 m वाले एक आयताकार लॉन के बीचो-बीच में एक आयताकार तालाब इस प्रकार बनाया जाना है कि तालाब के चारों ओर लगी घास वाले भाग का क्षेत्रफल 1184 m2 हो [आंकड़ा देखें]। तालाब की लंबाई और चौड़ाई ज्ञात कीजिए।

Solution
दिया गया है कि विमाओं 50 m × 40 m के एक आयताकार लॉन के केंद्र में एक आयताकार तालाब का निर्माण करना है।
तो, तालाब के चारों ओर तालाब और लॉन के बीच की दूरी समान होगी।
कहो x m
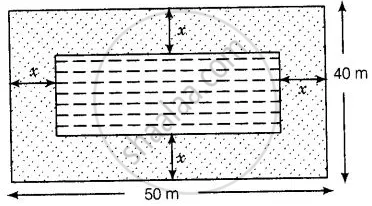
अब, आयताकार लॉन की लंबाई (l1) = 50 m और आयताकार लॉन की चौड़ाई (b1) = 40 m
आयताकार तालाब की लंबाई (l2)= 50 – (x + x) = 50 – 2x
और आयताकार तालाब की चौड़ाई (b2) = 40 – (x + x) = 40 – 2x
साथ ही, तालाब के चारों ओर घास का क्षेत्रफल = 1184 m2
आयताकार लॉन का क्षेत्रफल – आयताकार तालाब का क्षेत्रफल = तालाब के चारों ओर घास का क्षेत्रफल
l1 × b1 – l2 × b2 = 1184 ......[∵ आयत का क्षेत्रफल = लंबाई × चौड़ाई]
⇒ 50 × 40 – (50 – 2x)(40 – 2x) = 1184
⇒ 2000 – (2000 – 80x – 100x + 4x2) = 1184
⇒ 80x + 100x – 4x2 = 1184
⇒ 4x2 – 180x + 1184 = 0
⇒ x2 – 45x + 296 = 0
⇒ x2 – 37x – 8x + 296 = 0 ....[मध्य पद को विभाजित करके]
⇒ x(x – 37) – 8(x – 37) = 0
⇒ (x – 37)(x – 8) = 0
∴ x = 8
x = 37 पर,
तालाब की लंबाई और चौड़ाई क्रमशः – 24 और – 34 है, लेकिन लंबाई और चौड़ाई ऋणात्मक नहीं हो सकती।
तो, x = 37 संभव नहीं हो सकता।
∴ तालाब की लंबाई = 50 – 2x
= 50 – 2(8)
= 50 – 16
= 34 m
और तालाब की चौड़ाई = 40 – 2x
= 40 – 2(8)
= 40 – 16
= 24 m
अतः, तालाब की आवश्यक लंबाई और चौड़ाई क्रमशः 34 m और 24 m है।
APPEARS IN
RELATED QUESTIONS
निम्न स्थिति को द्विघात समीकरण के रूप में निरूपित कीजिए:
एक आयताकार भूखंड का क्षेत्रफल 528 m2 है। क्षेत्र की लंबाई (मीटरों में) चौड़ाई के दुगुने से एक अधिक है। हमें भूखंड की लंबाई और चौड़ाई ज्ञात करनी है।
यदि निम्नलिखित द्विघात समीकरण के मूल का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए:
2x2 - 7x + 3 = 0
यदि निम्नलिखित द्विघात समीकरण के मूल का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए:
2x2 + x - 4 = 0
यदि निम्नलिखित द्विघात समीकरण के मूल का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए:
`4x^2 + 4sqrt3x + 3 = 0`
नीचे दिए गए प्रश्न को द्विघात समीकरण के मूल, द्विघात सूत्र का उपयोग करके, ज्ञात कीजिए।
2x2 - 7x + 3 = 0
नीचे दिए गए प्रश्न को द्विघात समीकरण के मूल, द्विघात सूत्र का उपयोग करके, ज्ञात कीजिए।
2x2 + x - 4 = 0
नीचे दिए गए प्रश्न को द्विघात समीकरण के मूल, द्विघात सूत्र का उपयोग करके, ज्ञात कीजिए।
`4x^2 + 4sqrt3x + 3 = 0`
एक आयताकार खेत का विकर्ण उसकी छोटी भुजा से 60 मी अधिक लंबा है। यदि बड़ी भुजा छोटी भुजा से 30 मी अधिक हो, तो खेत की भुजाएँ ज्ञात कीजिए।
दो वर्गों के क्षेत्रफलों का योग 468 m2 है। यदि उनके परिमापों का अंतर 24 m हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
यदि ज़ेबा अपनी वास्तविक आयु से 5 वर्ष छोटी होती, तो उसकी आयु (वर्षो में) का वर्ग उसकी वास्तविक आयु के पाँच गुने से 11 वर्ष अधिक होता। उसकी वर्तमान आयु क्या है?
