Advertisements
Advertisements
प्रश्न
Visualise 2.665 on the number line, using successive magnification.
उत्तर
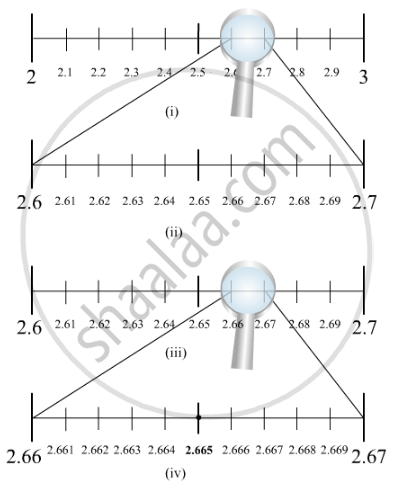
We know that 2.665 lies between 2 and 3. So, we divide the number line into 10 equal parts and mark each point of division. The first mark on the right of 2 will be 2.1 followed by 2.2 and so on.
The point left of 3 will be 2.9. Now, the magnified view of this will show that 2.665 lies between 2.6 and 2.7. So, our focus will be now 2.6 and 2.7. We divide this again into 10 equal parts. The first part will be 2.61 followed by 2.62 and so on.
We now magnify this again and find that 2.665 lies between 2.66 and 2.67. So, we magnify this portion and divide it again into 10 equal parts. The first part will represent 2.661, next will be 2.662 and so on.
So, 2.665 will be 5th mark in this subdivision as shown in the figure.
APPEARS IN
संबंधित प्रश्न
Visualise `4.bar26` on the number line, up to 4 decimal places.
Represent `sqrt3.5,` `sqrt9.4,` `sqrt10.5` on the real number line.
Every point on a number line represents
The number \[1 . \bar{{27}}\] in the form \[\frac{p}{q}\] , where p and q are integers and q ≠ 0, is
\[0 . \bar{{001}}\] when expressed in the form \[\frac{p}{q}\] (p, q are integers, q ≠ 0), is
Represent the following numbers on the number line
5.348
Represent the following numbers on the number line
`4.bar(73)` upto 4 decimal places
Represent the following number on the number line:
`(-12)/5`
Locate `sqrt(5), sqrt(10)` and `sqrt(17)` on the number line.
Represent geometrically the following number on the number line:
`sqrt(8.1)`
