Advertisements
Advertisements
प्रश्न
Visualise the representation of `5.3bar7` on the number line upto 5 decimal places, that is upto 5.37777.
उत्तर
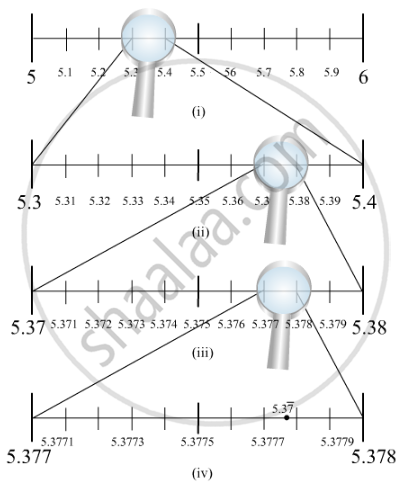
We know that `5.3bar7` will lie between 5 and 6. So, we locate `5.3bar7` between 5 and 6. We divide this portion of the number line between 5 and 6 into 10 equal parts and use a magnifying glass to visualize `5.3bar7` .
`5.3bar7` lies between 5.37 and 5.38. To visualize `5.3bar7` more accurately we use a magnifying glass to visualize between 5.377 and 5.378.
Again, we divide the portion between 5.377 and 5.378 into 10 equal parts and visualize more closely to represent `5.3bar7` as given in the figure. This is located between 5.3778 and 5.3777.
APPEARS IN
संबंधित प्रश्न
Represent `sqrt6,` `sqrt7,` `sqrt8` on the number line.
Represent `sqrt3.5,` `sqrt9.4,` `sqrt10.5` on the real number line.
Visualise 2.665 on the number line, using successive magnification.
The number 0.318564318564318564 ........ is:
The number \[1 . \bar{{27}}\] in the form \[\frac{p}{q}\] , where p and q are integers and q ≠ 0, is
\[23 . \bar{{43}}\] when expressed in the form \[\frac{p}{q}\] (p, q are integers q ≠ 0), is
\[0 . \bar{{001}}\] when expressed in the form \[\frac{p}{q}\] (p, q are integers, q ≠ 0), is
Locate `sqrt(5), sqrt(10)` and `sqrt(17)` on the number line.
Represent geometrically the following number on the number line:
`sqrt(5.6)`
Represent geometrically the following number on the number line:
`sqrt(2.3)`
