Question

What is meant by angular harmonic oscillation? Compute the time period of angular harmonic oscillation.

Answer 1

Time period and frequency of angular SHM: When a body is allowed to rotate freely about a given axis then the oscillation is known as the angular oscillation. The point at which the resultant torque acting on the body is taken to be zero is called mean position. If the body is displaced from the mean position, then the resultant torque acts such that it is proportional to the angular displacement and this torque has a tendency to bring the body towards the mean position.

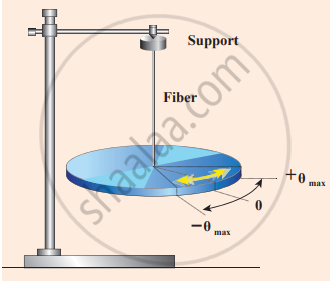
A body (disc) allowed to rotate freely about an axis

Let `vecθ` be the angular displacement of the body and the resultant torque `vecτ` acting on the body is

`vecτ ∝ vecθ` .............(1)

`vecτ = -κvec(θ)` ............(2)

κ is the restoring torsion constant, which is torque per unit angular displacement. If I is the moment of inertia of the body and `vecα` is the angular acceleration then

`vecτ = "I"vecα = -κvec(θ)` ...........(3)

But, `vecα = ("d"^2vec(θ))/("dt"^2)` and therefore,

`("d"^2vec(θ))/("dt"^2) = -κ/"I"  vec(θ)` .........(4)

This differential equation resembles a simple harmonic differential equation.

So, comparing equation (4) with simple harmonic motion given in equation α = `("d"^2"y")/"dt"^2 = -ω^2"y"`, we have

`ω = sqrt(κ/"I")` rad s⁻¹ .......(5)

The frequency of the angular harmonic motion is

f = `1/(2π) sqrt(κ/"I")` Hz ...........(6)

The time period is T = `2π sqrt(κ/"I")` seconds ..............(7)