Question

Describe Simple Harmonic Motion as a projection of uniform circular motion.

Answer 1

The projection of uniform circular motion on a diameter of SHM

Consider a particle of mass m moving with uniform speed v along the circumference of a circle whose radius is r in an anti-clockwise direction (as shown in the figure). Let us assume that the origin of the coordinate system coincides with the center O of the circle. If ω is the angular velocity of the particle and θ the angular displacement of the particle at any instant of time t, then θ = ωt. By projecting the uniform circular motion on its diameter gives a simple harmonic motion. This means that we can associate a map (or a relationship) between uniform circular (or revolution) motion with vibratory motion. Conversely, any vibratory motion or revolution can be mapped to uniform circular motion. In other words, these two motions are similar in nature.

Let us first project the position of a particle moving on a circle, on to its vertical diameter or on to a line parallel to the vertical diameter as shown in the figure. Similarly, we can do it for a horizontal axis or a line parallel to a horizontal axis.

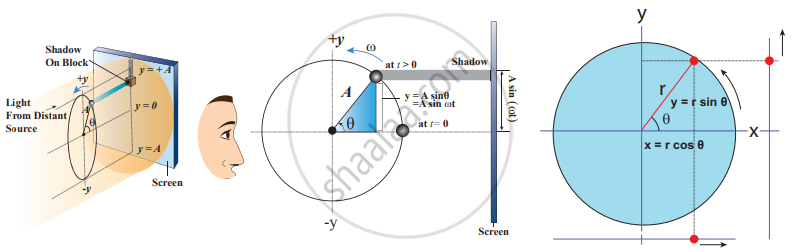
                                Projection of moving particle on a circle on a diameter

As a specific example, consider a spring-mass system (or oscillation of pendulum). When the spring moves up and down (or pendulum moves to and fro), the motion of the mass or bob is mapped to points on the circular motion.

Thus, if a particle undergoes uniform circular motion then the projection of the particle on the diameter of the circle (or on a line parallel to the diameter) traces straight-line motion which is simple harmonic in nature. The circle is known as the reference circle of the simple harmonic motion. The simple harmonic motion can also be defined as the motion of the projection of a particle on any diameter of a circle of reference.