Advertisements
Advertisements
प्रश्न
Write a pair of irrational numbers whose product is rational.
उत्तर
`(sqrt(3) + sqrt(2)) and (sqrt(3) - sqrt(2))` are irrational numbers whose product is rational.
Thus, we have
`(sqrt(3) + sqrt(2))(sqrt(3) - sqrt(2))`
= `(sqrt(3))^2 - (sqrt(2))^2`
= 3 - 2
= 1, which is a rational number.
APPEARS IN
संबंधित प्रश्न
Prove that the following is irrational:
`1/sqrt2`
Examine, whether the following number are rational or irrational:
`(sqrt2-2)^2`
Classify the numbers 3.121221222 as rational or irrational:
Mark the correct alternative in the following:
Which one of the following is a correct statement?
State, whether the following numbers is rational or not:
(√3 - √2)2
State, whether the following number is rational or not :
`( [√7]/[6sqrt2])^2`
Use method of contradiction to show that √3 and √5 are irrational numbers.
Classify the following number as rational or irrational with justification:
0.5918
Show that x is irrational, if x2 = 6.
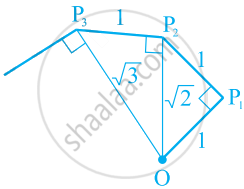
Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1 P2 perpendicular to OP1 of unit length. Now draw a line segment P2 P3 perpendicular to OP2. Then draw a line segment P3 P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn–1Pn by drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2, P3,...., Pn,.... ., and joined them to create a beautiful spiral depicting `sqrt2, sqrt3, sqrt4,` ...