Advertisements
Advertisements
प्रश्न
Write the solution set of the inequation |x − 1| ≥ |x − 3|.
उत्तर
\[\text{ We have }: \]
\[\left| x - 1 \right| \geq \left| x - 3 \right|\]
\[ \Rightarrow \left| x - 1 \right| - \left| x - 3 \right| \geq 0\]
\[\text{ The LHS of the inequation has two seperate modulus . Equating these to zero, we obtain x = 1, 3 as critical points } . \]
\[\text{ These points divide the real line in three regions, i . e } ( - \infty , 1], [1, 3], [3, \infty ) . \]
\[\text{ CASE 1: When } - \infty < x \leq 1, \text{ then } \left| x - 1 \right| = - (x - 1) and \left| x - 3 \right| = - (x - 3)\]
\[ \therefore \left| x - 1 \right| - \left| x - 3 \right| \geq 0\]
\[ \Rightarrow - (x - 1) - \left[ - (x - 3) \right] \geq 0\]
\[ \Rightarrow - x + 1 + x - 3 \geq 0\]
\[ \Rightarrow - 2 \geq 0\]
\[\text{ But this is not possible } . \]
\[\text{ CASE 2: When } 1 \leq x \leq 3, \text{ then } \left| x - 1 \right| = x - 1and \left| x - 3 \right| = - (x - 3)\]
\[ \therefore \left| x - 1 \right| - \left| x - 3 \right| \geq 0\]
\[ \Rightarrow x - 1 + x - 3 \geq 0\]
\[ \Rightarrow \Rightarrow 2x \geq 4\]
\[ \Rightarrow x \geq 2\]
\[ \Rightarrow x \in [2, \infty )\]
\[\text{ CASE 3: When } 3 \leq x < \infty , \text{ then } \left| x - 1 \right| = x - 1 and \left| x - 3 \right| = x - 3\]
\[ \therefore \left| x - 1 \right| - \left| x - 3 \right| \geq 0\]
\[ \Rightarrow x - 1 - x + 3 \geq 0 \]
\[ \Rightarrow 2 \geq 0\]
\[\text{ This is true } . \]
\[\text{ Hence, the solution to the given inequality comes from cases 2 and 3 } . \]
\[[2, \infty )U [3, \infty ) = [2, \infty )\]
\[ \therefore x \in [2, \infty )\]
APPEARS IN
संबंधित प्रश्न
Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2
Solve the following system of inequalities graphically: 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically: 2x + y≥ 6, 3x + 4y ≤ 12
Solve the following system of inequalities graphically: 2x – y > 1, x – 2y < –1
Solve the following system of inequalities graphically: x + y ≤ 6, x + y ≥ 4
Solve the following system of inequalities graphically: x + y ≤ 9, y > x, x ≥ 0
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: 2x + y≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solve the following system of inequalities graphically: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Find all pairs of consecutive odd positive integers, both of which are smaller than 10, such that their sum is more than 11.
A solution is to be kept between 86° and 95°F. What is the range of temperature in degree Celsius, if the Celsius (C)/ Fahrenheit (F) conversion formula is given by\[F = \frac{9}{5}C + 32\]
A solution is to be kept between 30°C and 35°C. What is the range of temperature in degree Fahrenheit?
To receive grade 'A' in a course, one must obtain an average of 90 marks or more in five papers each of 100 marks. If Shikha scored 87, 95, 92 and 94 marks in first four paper, find the minimum marks that she must score in the last paper to get grade 'A' in the course.
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If there are 640 litres of the 8% solution, how many litres of 2% solution will have to be added?
Write the set of values of x satisfying the inequation (x2 − 2x + 1) (x − 4) < 0.
Write the number of integral solutions of \[\frac{x + 2}{x^2 + 1} > \frac{1}{2}\]
Write the set of values of x satisfying the inequations 5x + 2 < 3x + 8 and \[\frac{x + 2}{x - 1} < 4\]
Solve each of the following system of equations in R.
\[5x - 7 < 3\left( x + 3 \right), 1 - \frac{3x}{2} \geq x - 4\]
Find the graphical solution of the following system of linear inequations:
x – y ≤ 0, 2x – y ≥ − 2
Find the graphical solution of the following system of linear inequations:
2x + 3y ≥ 12, – x + y ≤ 3, x ≤ 4, y ≥ 3
Find the graphical solution of the following system of linear inequations:
`"x"/60 + "y"/90 ≤ 1`, `"x"/120 + "y"/75 ≤ 1`, y ≥ 0, x ≥ 0
Solve the following system of inequalities `(2x + 1)/(7x - 1) > 5, (x + 7)/(x - 8) > 2`
Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
Solution set of x ≥ 0 and y ≤ 0 is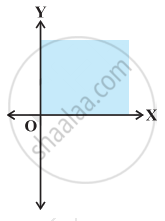
Solution set of x ≥ 0 and y ≤ 1 is