Advertisements
Advertisements
प्रश्न
Write the solution of the inequation\[\frac{x^2}{x - 2} > 0\]
उत्तर
\[\text{ We have }, \]
\[\frac{x^2}{x - 2} > 0\]
\[\text{ Equating both the numerator and the denominator with zero, we obtain x = 0 and x = 2 as critical points } . \]
\[\text{ Plotting these points on the real line, we see that the real line is divided into three regions } .

\[\text{ Therefore, the solution set of the given inequality is } x \in (2, \infty )\]
APPEARS IN
संबंधित प्रश्न
Solve the given inequality graphically in two-dimensional plane: 2x + y ≥ 6
Solve the given inequality graphically in two-dimensional plane: 3x + 4y ≤ 12
Solve the given inequality graphically in two-dimensional plane: x – y ≤ 2
Solve the given inequality graphically in two-dimensional plane: 3y – 5x < 30
Solve the given inequality graphically in two-dimensional plane: y < –2
Solve the inequalities and represent the solution graphically on number line:
5x + 1 > –24, 5x – 1 < 24
Solve the following inequalities and represent the solution graphically on number line:
3x – 7 > 2(x – 6), 6 – x > 11 – 2x
A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius/Fahrenheit (F) conversion formula is given by `F= 9/8` C + 32?
IQ of a person is given by the formula
IQ = `(MA)/(CA) xx100`
Where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6, 3x + 2y ≤ 6, x ≥ 0, y ≥ 0
Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x − y ≤ 1, x + 2y ≤ 8, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x + y ≥ 1, 7x + 9y ≤ 63, x ≤ 6, y ≤ 5, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
2x + 3y ≤ 35, y ≥ 3, x ≥ 2, x ≥ 0, y ≥ 0
Show that the solution set of the following linear inequations is empty set:
x + 2y ≤ 3, 3x + 4y ≥ 12, y ≥ 1, x ≥ 0, y ≥ 0
Find the linear inequations for which the shaded area in Fig. 15.41 is the solution set. Draw the diagram of the solution set of the linear inequations:
Show that the solution set of the following linear in equations is an unbounded set:
x + y ≥ 9
3x + y ≥ 12
x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
Solve the following systems of inequations graphically:
12x + 12y ≤ 840, 3x + 6y ≤ 300, 8x + 4y ≤ 480, x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
5x + y ≥ 10, 2x + 2y ≥ 12, x + 4y ≥ 12, x ≥ 0, y ≥ 0
Show that the solution set of the following system of linear inequalities is an unbounded region:
\[2x + y \geq 8, x + 2y \geq 10, x \geq 0, y \geq 0\]
Mark the correct alternative in each of the following:
If x\[<\]7, then
Find the linear inequalities for which the shaded region in the given figure is the solution set.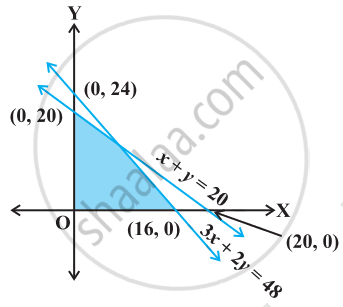
Graph of x < 3 is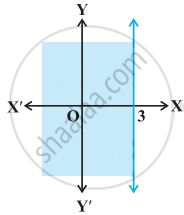
Graph of y ≤ 0 is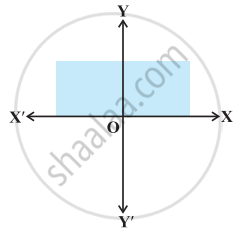
Solution set of x + y ≥ 0 is