Advertisements
Advertisements
प्रश्न
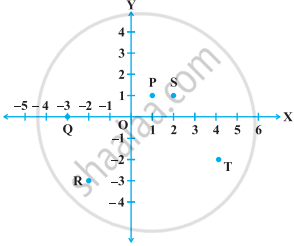
Write the coordinates of each of the points P, Q, R, S, T and O from the figure.
उत्तर
Here, points P and S lie in I quadrant so their both coordinates will be positive. Now, perpendicular distance of P from both axes is 1, so coordinates of P are (1, 1). Also, perpendicular distance of S from X-axis is 1 and from Y-axis is 2, so coordinates of S are (2, 1).
Point Q lies on X-axis in negative direction so its y-coordinate will be zero and x-coordinate will be –3. So, coordinates of Q are (–3, 0).
Point R lies in III quadrant, so its both coordinates will be negative. Now, its perpendicular distance from X-axis is 3 and from Y-axis is 2, so coordinates of point R are (–2, –3).
Point T lies in IV quadrant, so its x-coordinate will be positive and y-coordinate will be negative. Now, its perpendicular distance from X-axis is 2 and from Y-axis is 4, so coordinates of T are (4, –2). Point O is the intersection of both axes, so it is the origin and its coordinates are O(0, 0).
APPEARS IN
संबंधित प्रश्न
Plot the following point on the graph paper:
(4, −3)
Plot the following point on the graph paper:
(7, −4)
Plot the following points in the coordinate plane and join them. What is your conclusion about the resulting figure?
(0, −4) (0, −2) (0, 4) (0, 5)
On plotting the points O(0, 0), A(3, 0), B(3, 4), C(0, 4) and joining OA, AB, BC and CO which of the following figure is obtained?
Plot the following point in a graph sheet.
J(8, −4)
Use the graph to determine the coordinates where each figure is located.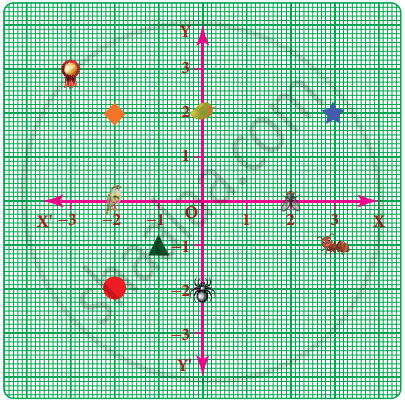
| a) Star | _______ |
| b) Bird | _______ |
| c) Red circle | _______ |
| d) Diamond | _______ |
| e) Triangle | _______ |
| f) Ant | _______ |
| g) Mango | _______ |
| h) Housefly | _______ |
| i) Medal | _______ |
| j) Spider | _______ |
Plot the following points and check whether they are collinear or not:
(0, 0), (2, 2), (5, 5)
Plot the points (x, y) given by the following table. Use scale 1 cm = 0.25 units
| x | 1.25 | 0.25 | 1.5 | – 1.75 |
| y | – 0.5 | 1 | 1.5 | – 0.25 |
Plot the points P(1, 0), Q(4, 0) and S(1, 3). Find the coordinates of the point R such that PQRS is a square.
Plot the points A(1, – 1) and B(4, 5). Draw a line segment joining these points. Write the coordinates of a point on this line segment between the points A and B.
