SSC (Marathi Medium) १० वीं कक्षा - Maharashtra State Board Important Questions for Mathematics 2 - Geometry [गणित २ - भूमिती]

'O' केंद्र असलेल्या वर्तुळाला P या बाह्यबिंदूतून AP ही A बिंदूपाशी स्पर्शिका काढली आहे. जर OP = 12 सेमी व ∠OPA = 30°, तर वर्तुळाची त्रिज्या ______ असेल.

'O' केंद्र असलेल्या वर्तुळाच्या जीवा AB व जीवा CD एकरूप आहेत. जर M(कंस AB) = 120°, तर M(कंस CD) काढा.

जर sinθ = cosθ, तर θ चे माप किती?

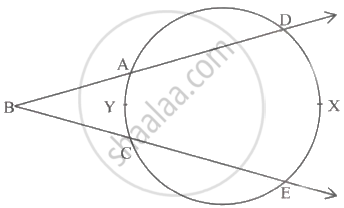
वरील आकृतीत, m(कंस DXE) = 105°, m(कंस AYC) = 47°, तर ∠DBE चे माप काढा.

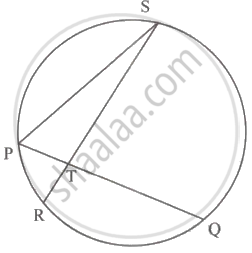
वरील आकृतीत जीवा PQ आणि जीवा RS एकमेकींना बिंदू T मध्ये छेदतात. जर ∠STQ = 58° आणि ∠PSR = 24°, तर ∠STQ = `1/2` [m(कंस PR) + m(कंस SQ)] या विधानाचा पडताळा घेण्यासाठी खालील कृती पूर्ण करा.

कृती:

ΔPTS मध्ये,

∠SPQ = ∠STQ - `square`  .......[∵ त्रिकोणाच्या बाहयकोनाचे प्रमेय.]

∴ ∠SPQ = 34°

∴ m(कंस QS) = 2 × `square`° = 68°  .......[∵ `square`]

तसेच m(कंस PR) = 2∠PSR = `square`°

∴ `1/2` [m(कंस QS) + m(कंस PR)] = `1/2` × `square`° = 58°  .......(I)

परंतु  ∠STQ = 58° .........(II) [दिलेले]

∴ `1/2` [m(कंस PR) + m(कंस QS)] = ∠______   ........[(I) व (II) वरून]

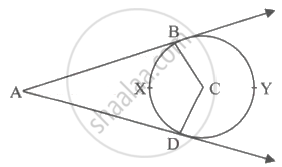
वरील आकृतीत, C केंद्र असलेल्या वर्तुळाला A या बाह्यबिंदूतून AB आणि AD हे स्पर्शिकाखंड काढले आहेत. तर सिद्ध करा:

∠A = `1/2` [m(कंस BYD) - m(कंस BXD)]

एका वर्तुळाच्या जीवा AB आणि जीवा CD परस्परांना वर्तुळाच्या अंतर्भागात बिंदू E मध्ये छेदतात. जर AE = 4, EB = 10, CE = 8, तर ED = किती?

एका वर्तुळाची त्रिज्या 5 सेमी आहे. तर त्या वर्तुळातील सर्वात मोठया जीवेची लांबी किती?

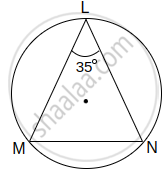
वरील आकृतीत ∠L = 35° असेल, तर

1. m(कंस MN) = किती?
2. m(कंस MLN) = किती?

उकल:

1. ∠L = `1/2` m(कंस MN) ............(अंतर्लिखित कोनाचे प्रमेय)
   ∴ `square = 1/2` m(कंस MN)
   ∴ 2 × 35 = m(कंस MN)
   ∴ m(कंस MN) = `square`
2. m(कंस MLN) = `square` - m(कंस MN) ...........(कंसाच्या मापाची व्याख्या)
   = 360° - 70°
   ∴ m(कंस MLN) = `square`

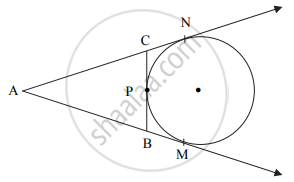
वरील आकृतिमध्ये दाखविल्याप्रमाणे, ΔABC च्या बाजू BC वरील P बिंदूत एक वर्तुळ बाहेरून स्पर्श करते. वाढवलेल्या रेषा AC व रेषा AB, त्या वर्तुळाला अनुक्रमे बिंदू N व बिंदू M मध्ये स्पर्श करतात. तर सिद्ध करा: AM = `1/2`(ΔABC ची परिमिती)

वरील आकृतीमध्ये, ∠ABC हा कंस ABC मधील आंतरलिखित कोन आहे. जर ∠ABC = 60°, तर m∠AOC काढा.

उकल:

∠ABC = `1/2` m(कंस AXC)  ...`square` 

60° = `1/2` m(कंस AXC) 

`square` = m(कंस AXC) 

परंतु m∠ AOC = m(कंस `square`)   ...(केंद्रीय कोनाचा गुणधर्म)

∴ m ∠AOC = `square`

O केंद्र असलेल्या वर्तुळाची AB जीवा आहे. AOC वर्तुळाचा व्यास आहे. स्पर्शिका AT वर्तुळाला बिंदू A मध्ये स्पर्श करते.

खालील प्रश्‍नांची उत्तरे लिहा:

1. वरील दिलेल्या माहितीवरून आकृती काढा.
2. ∠CAT व ∠ABC ची मापे काढा व त्याचे कारण लिहा.
3. ∠CAT व ∠ABC एकरूप आहेत का? स्पष्टीकरण लिहा.

3 सेमी त्रिज्या असलेल्या वर्तुळातील सर्वांत मोठ्या जीवेची लांबी किती?

बिंदू O केंद्र घेऊन 3 सेमी त्रिज्येचे वर्तुळ काढा. या वर्तुळास P या बाह्यबिंदूतून रेख PA व रेख PB हे स्पर्शिकाखंड असे काढा की ∠APB 70°.

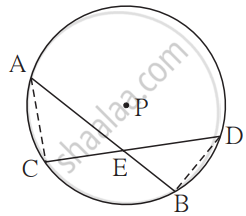
पक्ष:

केंद्र P असलेल्या वर्तुळाच्या जीवा AB आणि जीवा CD वर्तुळाच्या अंतर्भागात बिंदू E मध्ये छेदतात.

साध्य:

AE × EB = CE × ED

रचना:

रेख AC आणि रेख BD काढले.

रिकाम्या जागा भरून सिद्धता पूर्ण करा.

सिद्धता:

Δ CAE आणि Δ BDE मध्ये,

∠AEC ≅ ∠DEB    ...`square`

`square` ≅ ∠BDE     ...(एकाच वर्तुळकंसात अंतर्लिखित कोन)

∴ Δ CAE ~ Δ BDE    ...`square`

∴ `square/ ("DE") = ("CE")/square`    ...`square` 

∴ AE × EB = CE × ED

ΔABC ∼ ΔLMN, ΔABC असा काढा, की AB = 5.5 सेमी, BC = 6 सेमी, CA = 4.5 सेमी आणि `"BC"/"MN" = 5/4` तर ΔABC व ΔLMN काढा.

केंद्र P व त्रिज्या 3.2 सेमी असलेल्या वर्तुळाला त्यावरील M बिंदूतून स्पर्शिका काढा.

3.3 सेमी त्रिज्येचे वर्तुळ काढा. त्यामध्ये 6.6 सेमी लांबीची जीवा PQ काढा. बिंदू P व बिंदू Q मधून वर्तुळाला स्पर्शिका काढा. स्पर्शिकांबाबत तुमचे निरीक्षण नोंदवा.

4.1 सेमी त्रिज्या घेऊन एक वर्तुळ काढा. वर्तुळ केंद्रापासून 7.3 सेमी अंतरावरील बिंदूतून स्पर्शिका काढा.

ΔSHR ∼ ΔSVU, ΔSHR मध्ये SH = 4.5 सेमी, HR = 5.2 सेमी, SR = 5.8 सेमी, `"HS"/"SV" = 3/5`, तर ΔSVU काढा.