Question

2a भुजा के समबाहु त्रिभुज का आधार y-अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिंदु मूल बिंदु पर है। त्रिभुज के शीर्ष ज्ञात कीजिए।

Answer 1

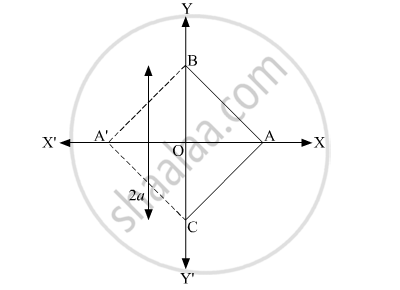
माना भुजा 2a वाला दिया गया समबाहु त्रिभुज ABC है।

इसलिए, AB = BC = CA = 2a

मान लीजिए कि आधार BC y-अक्ष पर इस प्रकार स्थित है कि BC का मध्य-बिंदु मूल बिंदु पर है।

यानी, BO = OC = a, जहां O मूल है।

अब, यह स्पष्ट है कि बिंदु C के निर्देशांक (0, a) हैं, जबकि बिंदु B के निर्देशांक (0, –a) हैं।

यह ज्ञात है कि किसी समबाहु त्रिभुज के शीर्ष को उसकी सम्मुख भुजा के मध्य - बिंदु से मिलाने वाली रेखा लम्ब होती है।

इसलिए, शीर्ष A, y - अक्ष पर स्थित है।

पाइथागोरस प्रमेय को ΔAOC पर लागू करने पर, हमें प्राप्त होता है,

(AC)² = (OA)² + (OC)²

⇒ (2a)² = (OA)² + a²

⇒ 4a² – a² = (OA)²

⇒ (OA)² = 3a²

⇒ OA = `sqrt3`

∴ बिंदु A के निर्देशांक = `(± sqrt(3a),0)`

इस प्रकार, दिए गए समबाहु त्रिभुज के शीर्ष हैं (0, -a) और `(sqrt(3a),0)` या (0, a), (0, -a) और `(-sqrt(3a),0 )`.