Advertisements
Advertisements
प्रश्न
कार्तीय तल में एक चतुर्भुज खींचिए जिसके शीर्ष (−4, 5), (0, 7), (5, –5) और (−4, –2) हैं। इसका क्षेत्रफल भी ज्ञात कीजिए।
उत्तर
मान लीजिए ABCD शीर्ष A (-4, 5), B (0, 7), C (5, -5), और D (-4, -2) वाला चतुर्भुज है।
फिर, कार्तीय तल पर A, B, C और D को आलेखित करके और AB, BC, CD और DA को जोड़कर, दिए गए चतुर्भुज को इस प्रकार खींचा जा सकता है
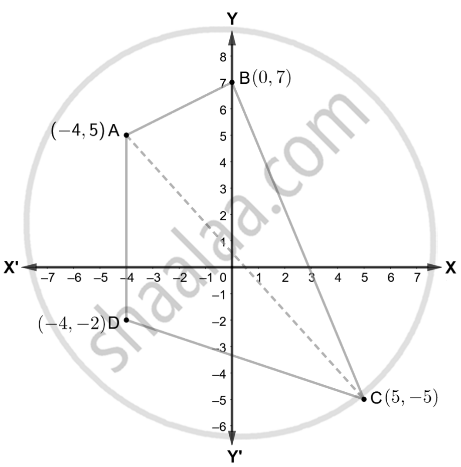
चतुर्भुज ABCD का क्षेत्रफल ज्ञात करने के लिए, हम एक विकर्ण, मान लीजिए AC, खींचते हैं।
उसी प्रकार से, क्षेत्रफल (ABCD) = क्षेत्रफल (ΔABC) + क्षेत्रफल (ΔACD)
हम जानते हैं कि एक त्रिभुज का क्षेत्रफल (x1, y1), (x2, y2), and (x3, y3) है
`1/2 |x_1 (y_2 - y_3) + x_2 (y_3 - y_1) + x_3 (y_1 - y_2)|`
इसलिए, ΔABC का क्षेत्रफल
= `1/2 |-4 (7 + 5) + 0 (-5 -5) +5 (5 - 7)|"इकाई"^2`
= `1/2 |-4 (12) + 5 (-2)| "इकाई"^2`
= `1/2 |-48 - 10| "इकाई"^2`
= `1/2 |-58| "इकाई"^2`
= `1/2 xx 58 "इकाई"^2`
= 29 इकाई2
ΔACD का क्षेत्रफल
= `1/2 |-4 (-5 + 2) + 5 (-2 -5) + (-4) (5 + 5)| "इकाई"^2`
= `1/2 |-4 (-3) + 5 (-7) -4 (10)| "इकाई"^2`
= `1/2 |12 - 35 - 40| "इकाई"^2`
= = `1/2 |-63| "इकाई"^2`
= `63/2 "इकाई"^2`
इस प्रकार, क्षेत्रफल (ABCD) = `29 + 63/2 "इकाई"^2 = (58 + 63)/2 "इकाई"^2 = (121)/2 "इकाई"^2`
APPEARS IN
संबंधित प्रश्न
2a भुजा के समबाहु त्रिभुज का आधार y-अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिंदु मूल बिंदु पर है। त्रिभुज के शीर्ष ज्ञात कीजिए।
P(x1, y1) और Q(x2, Y2) के बीच की दूरी ज्ञात कीजिए जब:
- PQ, y-अक्ष के समांतर है।
- PQ, x-अक्ष के समांतर है।
x-अक्ष पर एक बिंदु ज्ञात कीजिए जो (7, 6) और (3, 4) बिंदुओं से समान दूरी पर है।
