Advertisements
Advertisements
प्रश्न
30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the another to form a cylindrical solid. Find volume of the cylinder so formed.
उत्तर
Given, radius of a circular plate, r = 14 cm
Thickness of a circular plate = 3 cm
Thickness of 30 circular plates = 30 × 3 = 90 cm
Since, 30 circular plates are placed one above the another to form a cylindrical solid.
Then, Height of the cylindrical solid, h = Thickness of 30 circular plates = 90 cm
Volume of the cylinder so formed = πr2h
= `(22/7) xx (14)^2 xx 90`
= `(22/7) xx 14 xx 14 xx 90`
= 22 × 28 × 90
= 55440 cm3
Hence, the volume of the cylinder so formed is 55440 cm3.
APPEARS IN
संबंधित प्रश्न
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 m s–1. Calculate, in minutes, the time it takes to fill the tank.
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find :
- the volume
- the total surface area.
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the area covered by the cylinder in `4 1/2` seconds.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
- radius of the vessel.
- height of the vessel.
- wetted surface area of the vessel when it is half-filled with water.
Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.
A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
The ratio of radii of two cylinders is 1 : 2 and heights are in the ratio 2 : 3. The ratio of their volumes is ______.
The volume of a cylinder becomes ______ the original volume if its radius becomes half of the original radius.
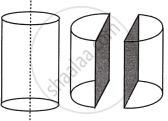
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.