Advertisements
Advertisements
प्रश्न
उत्तर
9.5 सेमी लंबाई का एक रेखाखंड और उसका लंब समद्विभाजक बनाने के लिए नीचे दिए गए चरणों का पालन किया जाएगा।
- 9.5 सेमी का एक रेखाखंड `overline"PQ"` खींचिए।

- P को केंद्र मानकर परकार का उपयोग करके एक वृत्त खींचिए। वृत्त की त्रिज्या `overline"PQ"` की लंबाई के आधे से अधिक होनी चाहिए।
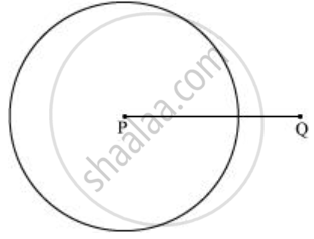
- पहले की तरह ही त्रिज्या से, बिंदु Q को केंद्र मानकर परकार का उपयोग करके एक और वृत्त बनाएं। मान लीजिए कि यह पिछले वृत्त को R और S पर काटता है।
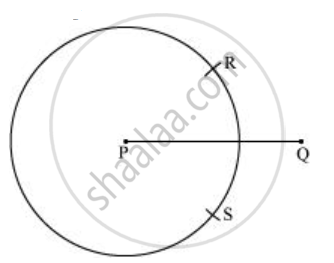
- आरएस से जुड़ें। `overline"RS"` समरूपता का अक्ष है अर्थात रेखा `overline"PQ"` का लंब समद्विभाजक है।

APPEARS IN
संबंधित प्रश्न
एक रेखाखंड `overline"XY"` का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है।
- इस लंब समद्विभाजक पर कोई बिंदु P लीजिए। जाँच कीजिए कि PX = PY है।
- यदी M रेखाखंड `overline"XY"` का मध्य बींदु है, तो MX और XY के विषय में आप क्या कह सकते हैं?
लंबाई 12.8 सेमी वाला एक रेखाखंड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कौजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
केंद्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा `overline"AB"` खींचिए। इस जिवा `overline"AB"` का लंब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केंद्र C से होकर जाता है।
4 सभी ज्रिज्या का एक वृत्त खोचिए। इसका काई दो जीवाएँ खांचिए। इन दोनों जीवाओं के लंब समद्रिभाजक खींचिए। ये कहाँ मिलते हैं?
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर एक बिंदु A और दूसरी भुजा पर एक अन्य बिंदु B इस परकार लीजिए कि OA = OB है। OA और OB के लंब समद्विभाजक खींचिए। मान लीजिए ये P पर प्रतिछेदित करते हैं क्या PA = PB है?
