Advertisements
Advertisements
प्रश्न
एक रेखाखंड `overline"XY"` का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है।
- इस लंब समद्विभाजक पर कोई बिंदु P लीजिए। जाँच कीजिए कि PX = PY है।
- यदी M रेखाखंड `overline"XY"` का मध्य बींदु है, तो MX और XY के विषय में आप क्या कह सकते हैं?
उत्तर
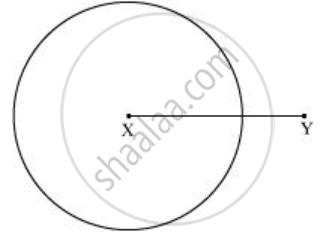
- 10.3 सेमी का एक रेखाखंड `overline"XY"` खींचिए।

- बिंदु X को केंद्र मानकर परकार की सहायता से एक वृत्त खींचिए। वृत्त की त्रिज्या `overline"XY"` की लंबाई के आधे से अधिक होनी चाहिए।
-
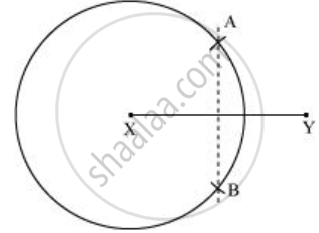
पहले की तरह ही त्रिज्या के साथ, बिंदु Y को केंद्र मानकर परकार का उपयोग करके एक और वृत्त बनाएं। मान लीजिए कि यह पिछले वृत्त को A और B पर काटता है।

- `overline"AB"` से जुड़ें. `overline"AB"` सममिति का अक्ष है।
-
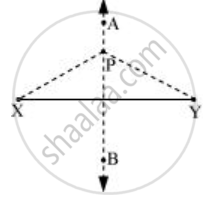
`overline"AB"` पर कोई बिंदु P लीजिए। हम पाएंगे कि PX और PY की लंबाई के माप समान हैं।
ऐसा इसलिए है क्योंकि `overline"AB"` सममिति का अक्ष है। अत: `overline"AB"` पर स्थित कोई भी बिंदु `overline"XY"` के दोनों सिरों से समान दूरी पर होगा।
-
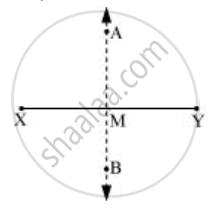
M, `overline"XY"` का मध्य-बिंदु है। लम्ब समद्विभाजक `overline"AB"` बिंदु M से होकर गुजरेगा। इसलिए, `overline"XY"` की लंबाई `overline"MX"` से दोगुनी है।
या 2MX = XY
APPEARS IN
संबंधित प्रश्न
लंबाई 12.8 सेमी वाला एक रेखाखंड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कौजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
केंद्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा `overline"AB"` खींचिए। इस जिवा `overline"AB"` का लंब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केंद्र C से होकर जाता है।
4 सभी ज्रिज्या का एक वृत्त खोचिए। इसका काई दो जीवाएँ खांचिए। इन दोनों जीवाओं के लंब समद्रिभाजक खींचिए। ये कहाँ मिलते हैं?
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर एक बिंदु A और दूसरी भुजा पर एक अन्य बिंदु B इस परकार लीजिए कि OA = OB है। OA और OB के लंब समद्विभाजक खींचिए। मान लीजिए ये P पर प्रतिछेदित करते हैं क्या PA = PB है?
