Advertisements
Advertisements
प्रश्न
A 150 m long train is moving with constant velocity of 12.5 m/s. Find the equation of the motion of the train
उत्तर
Length of the train = 150 m
Constant velocity of the train = 12.5 m/s
The equation of motion of the train:
Take time in seconds along the x-axis and distance in meters along the y-axis.
Let the train be at the origin.
∴ Length of the train = 150 m is the negative y-intercept
b = -150
The slope of the motion of the train m = 12.5 m/s
The equation of the line with slope-intercept form is
y = mx + b
∴ y = 12.5x – 150
which is the required equation of motion of the train.
APPEARS IN
संबंधित प्रश्न
Find the slope of the following line which passes through the points:
C(−2, 3), D(5, 7)
Find the slope of the following line which passes through the points:
G(7, 1), H(−3, 1)
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured anticlockwise
Find the acute angle between the X-axis and the line joining points A(3, −1) and B(4, −2).
A line passes through points A(x1, y1) and B(h, k). If the slope of the line is m then show that k − y1 = m(h − x1)
Find the equation of the lines passing through the point (1, 1) with y-intercept (– 4)
Find the equation of the lines passing through the point (1, 1) and the perpendicular from the origin makes an angle 60° with x-axis
If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that `1/("p"^3) = 1/("a"^2) + 1/("b"^2)`
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the value of C for 98.6°F
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find the distance between the place and the target
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find time taken to hit the target
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using any other method
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Find the equation relating the quantity of gas in the cylinder to the days
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the minimum total length of the escalator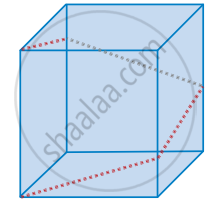
Choose the correct alternative:
The line (p + 2q)x + (p − 3q)y = p − q for different values of p and q passes through the point
The distance of the origin from the centroid of the triangle whose two sides have the equations. x – 2y + 1 = 0 and 2x – y – 1 = 0 and whose orthocenter is `(7/3. 7/3)` is ______.
The locus of the point of intersection of the lines xcosα + ysinα = α and xsinα – ycosα = b(where α is a variable) is ______.
The coordinates of vertices of base BC of an isosceles triangle ABC are given by B(1, 3) and C(–2, 7) which of the following points can be the possible coordinates of the vertex A?
If planes x – cy – bz = 0, cx – y + az = 0 and bx + ay – z = 0 pass through a straight line then a2 + b2 + c2 = ______.
