Advertisements
Advertisements
प्रश्न
A baloon filled with helium rises against gravity increasing its potential energy. The speed of the baloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy? You can neglect viscous drag of air and assume that density of air is constant.
उत्तर
Because the pulling viscous force of the air on the balloon is ignored, there is
Net Buoyant Force = `Vpg`
The volume of air displaced × net density upward × g
= `V(p_(ar) - p_(He)) g(upward)`
Let a be the upward acceleration on the balloon then
`ma = V(p_(ag) - p_(He)) g`
Where m = mass of the balloon
V = Volume of air displacement by balloon
= Volume of balloon
`p_(air)` = density of air
`p_(He)` = density of helium
`m (dv)/(dt) = V * (p_(ar) - p_(He)) g`
`mdv = V * (p_(air) - p_(He)) g * dt`
Integrating both sides `mv = V * (p_(ar) - p_(He)) g t`
`v = V/m (p_(air) - p_(He)) g t`
KE of balloon = `1/2 mv^2`
`1/2 mv^2 = 1/2 m v^2/m^2 (p_(air) - p_(He))^2g^2t^2`
= `V^2/(2m) (p_(air) - p_(He))^2g^2t^2` ......(ii)
If the balloon rises to a height h, from (i)
`a = V/m (p_(ai) - p_(he)) g`
`h = ut + 1/2 at^2 = 0.t + 1/2 [V/m (p_(ai) - p_(Bb))g]t^2`
∴ `h = V/(2m) (p_(ar) - p_(He)) g t^2`
Rearranging the words of (ii) according to h in (ii) and (iii) (iii)
`1/2 mv^2 = {V/(2m) (P_(air) - p_(He)) g t^2} * V(P_(air) - p_(He)) g`
`1/2 mv^2 = {h} * V (p_(air) - p_(He)) g`
`1/2 mv^2 = V * (p_(at) - p_(He)) gh`
`1/2 mv^2 = Vp_(air) gh - Vp_(He) = gh`
`1/2 mv^2 + p_(He)V gh = p_(av) V gh`
`KE_(balloon) + PE_(ballon)` = Change in PE of air.
As a result, as the balloon rises, an equivalent volume of air falls, increasing the balloon's PE and KE at the expense of the air's PE (which come down).
APPEARS IN
संबंधित प्रश्न
A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated.
- How much work does she do against the gravitational force?
- Fat supplies 3.8 x 107J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?
A heavy stone is thrown in from a cliff of height h in a given direction. The speed with which it hits the ground
(a) must depend on the speed of projection
(b) must be larger than the speed of projection
(c) must be independent of the speed of projection
(d) may be smaller than the speed of projection.
You lift a suitcase from the floor and keep it on a table. The work done by you on the suitcase does not depend on
(a) the path taken by the suitcase
(b) the time taken by you in doing so
(c) the weight of the suitcase
(d) your weight
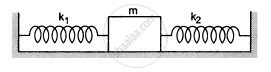
A block of mass m is attached to two unstretched springs of spring constants k1 and k2 as shown in the following figure. The block is displaced towards the right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.
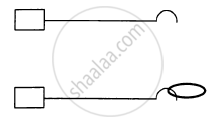
A small heavy block is attached to the lower end of a light rod of length l which can be rotated about its clamped upper end. What minimum horizontal velocity should the block be given so that it moves in a complete vertical circle?
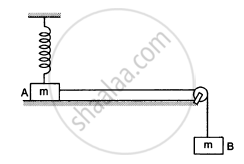
Figure following shows a light rod of length l rigidly attached to a small heavy block at one end and a hook at the other end. The system is released from rest with the rod in a horizontal position. There is a fixed smooth ring at a depth h below the initial position of the hook and the hook gets into the ring as it reaches there. What should be the minimum value of h so that the block moves in a complete circle about the ring?
Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track as shown in figure.
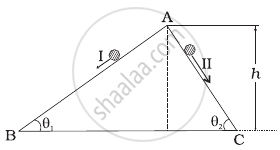
Which of the following statement is correct?
Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case?
A single conservative force acts on a body of mass 1 kg that moves along the x-axis. The potential energy U(x) is given by U (x) = 20 + (x - 2)2, where x is in meters. At x = 5.0 m the particle has a kinetic energy of 20 J, then the maximum kinetic energy of body is ______ J.
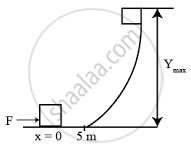
A force shown in the F-x graph is applied to a 5 kg cart, which then coasts up a ramp as shown. The maximum height, ymax is ______ m, at which the cart can reach.
(g = 10 m/s2)