Advertisements
Advertisements
प्रश्न
Two identical steel cubes (masses 50 g, side 1 cm) collide head-on face to face with a speed of 10 cm/s each. Find the maximum compression of each. Young’s modulus for steel = Y = 2 × 1011 N/m2.
उत्तर
Let m = 50 g = 50 × 10–3 kg
Side = L = 1 cm = 0.01 m
Speed = v = 10 cm/s = 0.1 m/s
Young's modulus = Y = 2 × 1011 N/m2
Maximum compression ΔL = ?
In this case, all KE will be converted to PE
By Hooke's law, `F/A = Y (ΔL)/L`
Where A is the surface area and L is the length of the side of the cube. If k is spring or compression constant, then
Force F = kΔL
∴ k = `Y A/L = YL`
Initial KE = `2 xx 1/2 mv^2 = 5 xx 10^-4` J
Final PE = `2 xx 1/2 k (ΔL)^2`
∴ ΔL = `sqrt((KE)/k)`
= `sqrt((KE)/(YL))`
= `sqrt((5 xx 10^-4)/(2 xx 10^11 xx 0.1))`
= 1.58 × 10–7 ......[∵ PE = KE]
APPEARS IN
संबंधित प्रश्न
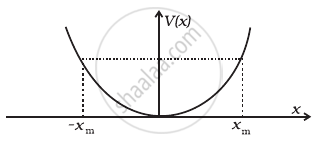
The potential energy function for a particle executing linear simple harmonic motion is given by V(x) =`(kx^2)/2`, where k is the force constant of the oscillator. For k = 0.5 N m–1, the graph of V(x) versus x is shown in the figure. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.

A body of mass 0.5 kg travels in a straight line with velocity v = `ax^(3/2)` where a = `5 m^(1/2)` s-1. What is the work done by the net force during its displacement from x = 0 to x = 2 m?
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is \[\frac{1}{2}k x^2\] . The possible cases are
(a) at spring was initially compressed by a distance x and was finally in its natural length
(b) it was initially stretched by a distance x and and finally was in its natural length
(c) it was initially in its natural length and finally in a compressed position
(d) it was initially in its natural length and finally in a stretched position.
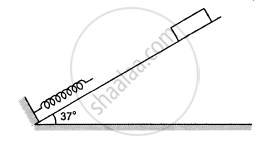
Following figure shows a spring fixed at the bottom end of an incline of inclination 37°. A small block of mass 2 kg starts slipping down the incline from a point 4⋅8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find (a) the friction coefficient between the plane and the block and (b) the spring constant of the spring. Take g = 10 m/s2.
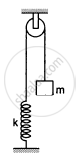
Consider the situation shown in the following figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the pulley, find the maximum elongation of the spring.
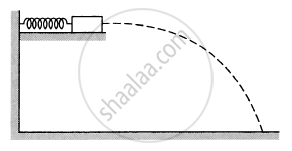
A block of mass m sliding on a smooth horizontal surface with a velocity \[\vec{\nu}\] meets a long horizontal spring fixed at one end and with spring constant k, as shown in following figure following. Find the maximum compression of the spring. Will the velocity of the block be the same as \[\vec{\nu}\] when it comes back to the original position shown?

A small block of mass 100 g is pressed against a horizontal spring fixed at one end to compress the spring through 5 cm (figure following). The spring constant is 100 N/m. When released, the block moves horizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
If a spring extends by x on loading, then energy stored by the spring is (T is the tension in the spring and k is the spring constant)
The potential energy function for a particle executing linear SHM is given by `V(x) = 1/2 kx^2` where k is the force constant of the oscillator (Figure). For k = 0.5 N/m, the graph of V(x) versus x is shown in the figure. A particle of total energy E turns back when it reaches `x = ±x_m`. If V and K indicate the P.E. and K.E., respectively of the particle at `x = +x_m`, then which of the following is correct?
A curved surface is shown in figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.

With the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.
- For which balls is total mechanical energy conserved?
- Which ball (s) can reach D?
- For balls which do not reach D, which of the balls can reach back A?
