Advertisements
Advertisements
प्रश्न
Two identical steel cubes (masses 50 g, side 1 cm) collide head-on face to face with a speed of 10 cm/s each. Find the maximum compression of each. Young’s modulus for steel = Y = 2 × 1011 N/m2.
उत्तर
Let m = 50 g = 50 × 10–3 kg
Side = L = 1 cm = 0.01 m
Speed = v = 10 cm/s = 0.1 m/s
Young's modulus = Y = 2 × 1011 N/m2
Maximum compression ΔL = ?
In this case, all KE will be converted to PE
By Hooke's law, `F/A = Y (ΔL)/L`
Where A is the surface area and L is the length of the side of the cube. If k is spring or compression constant, then
Force F = kΔL
∴ k = `Y A/L = YL`
Initial KE = `2 xx 1/2 mv^2 = 5 xx 10^-4` J
Final PE = `2 xx 1/2 k (ΔL)^2`
∴ ΔL = `sqrt((KE)/k)`
= `sqrt((KE)/(YL))`
= `sqrt((5 xx 10^-4)/(2 xx 10^11 xx 0.1))`
= 1.58 × 10–7 ......[∵ PE = KE]
APPEARS IN
संबंधित प्रश्न
The potential energy function for a particle executing linear simple harmonic motion is given by V(x) =`(kx^2)/2`, where k is the force constant of the oscillator. For k = 0.5 N m–1, the graph of V(x) versus x is shown in the figure. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.

When a conservative force does positive work on a body, the potential energy of the body ______.
The two ends of a spring are displaced along the length of the spring. All displacement have equal magnitudes. In which case or cases the tension or compression in the spring will have a maximum magnitude ?
(a) the right end is displaced towards right and the left end towards left
(b) both ends are displaced towards right
(c) both ends are displaced towards left
(d) the right end is displaced towards left and the left end towards right.
Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is \[\frac{1}{2}k x^2\] . The possible cases are
(a) at spring was initially compressed by a distance x and was finally in its natural length
(b) it was initially stretched by a distance x and and finally was in its natural length
(c) it was initially in its natural length and finally in a compressed position
(d) it was initially in its natural length and finally in a stretched position.
A block of mass m moving at a speed ν compresses a spring through a distance x before its speed is halved. Find the spring constant of the spring.
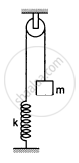
Consider the situation shown in the following figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the pulley, find the maximum elongation of the spring.
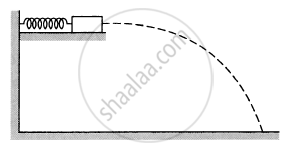
A small block of mass 100 g is pressed against a horizontal spring fixed at one end to compress the spring through 5 cm (figure following). The spring constant is 100 N/m. When released, the block moves horizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero.
A curved surface is shown in figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.

With the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.
- For which balls is total mechanical energy conserved?
- Which ball (s) can reach D?
- For balls which do not reach D, which of the balls can reach back A?
