Advertisements
Advertisements
प्रश्न
A rocket accelerates straight up by ejecting gas downwards. In a small time interval ∆t, it ejects a gas of mass ∆m at a relative speed u. Calculate KE of the entire system at t + ∆t and t and show that the device that ejects gas does work = `(1/2)∆m u^2` in this time interval (neglect gravity).
उत्तर
Let M be the mass of the rocket at any time t and v1 the velocity of the rocket at the same time t.
Let ∆m = mass of gas ejected in time interval ∆t.
The relative speed of gas ejected = u.
Consider at time t + ∆t
(KE)t + ∆t = KE of rocket + KE of gas
= `1/2 (M - ∆m) (v + ∆v)^2 + 1/2 ∆m (v - u)^2`
= `1/2 Mv^2 + Mv ∆v - ∆mvu + 1/2 ∆m u^2`
(KE)t = KE of the rocket at time t = `1/2 Mv^2`
∆K = (KE)t + ∆t – (KE)t
= (M∆v ∆mu)v + `1/2` ∆mu2
Since action-reaction forces are equal.
Hence, `M (dv)/(dt) = (dm)/(dt)|u|`
⇒ M∆v = ∆mu
∆K = `1/2` ∆mu2
Now, by work-energy theorem,
∆K = ∆W
⇒ ∆W = `1/2` ∆mu2
APPEARS IN
संबंधित प्रश्न
In a factory, 2000 kg of metal needs to be lifted by an engine through a distance of 12 m in 1 minute. Find the minimum horsepower of the engine to be used.
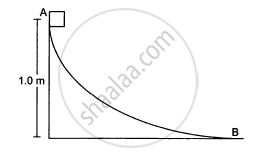
A block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (In the following figure). The rough surface has a friction coefficient of 0⋅20 with the block. If the block starts slipping on the track from a point 1⋅0 m above the horizontal surface, how far will it move on the rough surface?
A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed 10 cm shorter than its natural length and the system is released from this position. How high does the block rise ? Take g = 10 m/s2.
A simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angle of 37° with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.
Following figure following shows a smooth track, a part of which is a circle of radius R. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

A heavy particle is suspended by a 1⋅5 m long string. It is given a horizontal velocity of \[\sqrt{57} \text{m/s}\] (a) Find the angle made by the string with the upward vertical when it becomes slack. (b) Find the speed of the particle at this instant. (c) Find the maximum height reached by the particle over the point of suspension. Take g = 10 m/s2.
A smooth sphere of radius R is made to translate in a straight line with a constant acceleration a. A particle kept on the top of the sphere is released at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle θ it slides.
A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
- Work done by all forces on man is equal to the rise in potential energy mgL.
- Work done by all forces on man is zero.
- Work done by the gravitational force on man is mgL.
- The reaction force from a step does not do work because the point of application of the force does not move while the force exists.
A bullet of mass m fired at 30° to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of bullet after it emerges out of the target?
- The velocity of the bullet will be reduced to half its initial value.
- The velocity of the bullet will be more than half of its earlier velocity.
- The bullet will continue to move along the same parabolic path.
- The bullet will move in a different parabolic path.
- The bullet will fall vertically downward after hitting the target.
- The internal energy of the particles of the target will increase.
Suppose the average mass of raindrops is 3.0 × 10–5 kg and their average terminal velocity 9 ms–1. Calculate the energy transferred by rain to each square metre of the surface at a place which receives 100 cm of rain in a year.
