Advertisements
Advertisements
प्रश्न
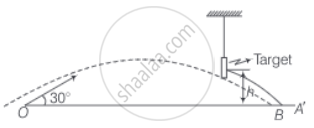
A bullet of mass m fired at 30° to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of bullet after it emerges out of the target?
- The velocity of the bullet will be reduced to half its initial value.
- The velocity of the bullet will be more than half of its earlier velocity.
- The bullet will continue to move along the same parabolic path.
- The bullet will move in a different parabolic path.
- The bullet will fall vertically downward after hitting the target.
- The internal energy of the particles of the target will increase.
उत्तर
b, d and f
Explanation:
Consider the adjacent diagram for the given situation in the question.
b. Conserving energy between "O" and "A"
`U_i + K_i = U_f + K_f`
⇒ `0 + 1/2 mv^2 = mgh + 1/2 mv^'`
⇒ `(v^')^2/2 = v^2/2 = - gh`
⇒ `(v^')^2 = v^2 - 2 gh`
⇒ `v^' = sqrt(v^2 - 2 gh)` ......(i)
Where v' is the speed of the bullet just before hitting the target. Let speed after emerging from the target is v" then,
By question, = `1/2 (mv^")^2 = 1/2[1/2 m(v^')^2]`
= `1/2 m(v^")^2`
= `1/4 m(v^')^2`
= `1/4 m[v^2 - 2 gh]`
⇒ `(v^")^2 = (v^2 - 2 gh)/2 = v^2/2 - gh`
⇒ `v^" = sqrt(v^2/2 - gh)` .....(ii)
From equations (i) and (ii)
`v^'/v^" = (sqrt(v^2 - 2 gh))/(sqrt(v^2 - 2 gh)/(sqrt(2))) = sqrt(2)`
⇒ `v^" = v^'/sqrt(2) = v^2 (v^'/2)`
⇒ `v^"/(v^'/2) = sqrt(2)` = 1.414 > 1
⇒ `v^" > v^'/2`
Hence, after emerging from the target velocity of the bullet (v") is more than half of its earlier velocity v’ (velocity before emerging into the target).
d. As the velocity of the bullet changes to v’ which is less than v1 hence, the path, followed will change and the bullet reaches point B instead of A', as shown in the figure.
f. As the bullet is passing through the target the loss in energy of the bullet is transferred to particles of the target. Therefore, their internal energy increases.
APPEARS IN
संबंधित प्रश्न
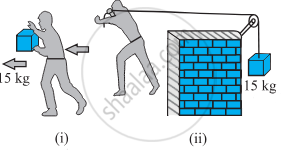
In Figure (i) the man walks 2 m carrying a mass of 15 kg on his hands. In Figure (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
A block of mass 30 kg is being brought down by a chain. If the block acquires a speed of 40 cm/s in dropping down 2 m, find the work done by the chain during the process.
A heavy particle is suspended by a 1⋅5 m long string. It is given a horizontal velocity of \[\sqrt{57} \text{m/s}\] (a) Find the angle made by the string with the upward vertical when it becomes slack. (b) Find the speed of the particle at this instant. (c) Find the maximum height reached by the particle over the point of suspension. Take g = 10 m/s2.
A simple pendulum of length L with a bob of mass m is deflected from its rest position by an angle θ and released (following figure). The string hits a peg which is fixed at a distance x below the point of suspension and the bob starts going in a circle centred at the peg. (a) Assuming that initially the bob has a height less than the peg, show that the maximum height reached by the bob equals its initial height. (b) If the pendulum is released with \[\theta = 90^\circ \text{ and x = L}/2\] , find the maximum height reached by the bob above its lowest position before the string becomes slack. (c) Find the minimum value of x/L for which the bob goes in a complete circle about the peg when the pendulum is released from \[\theta = 90^\circ \]

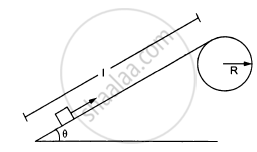
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. Find the minimum projection-speed \[\nu_0\] for which the particle reaches the top of the track.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
A smooth sphere of radius R is made to translate in a straight line with a constant acceleration a. A particle kept on the top of the sphere is released at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle θ it slides.
An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because ______.
Give example of a situation in which an applied force does not result in a change in kinetic energy.
Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare?
