Advertisements
Advertisements
Question
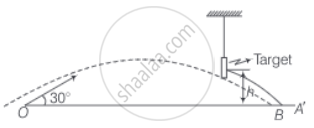
A bullet of mass m fired at 30° to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of bullet after it emerges out of the target?
- The velocity of the bullet will be reduced to half its initial value.
- The velocity of the bullet will be more than half of its earlier velocity.
- The bullet will continue to move along the same parabolic path.
- The bullet will move in a different parabolic path.
- The bullet will fall vertically downward after hitting the target.
- The internal energy of the particles of the target will increase.
Advertisements
Solution
b, d and f
Explanation:
Consider the adjacent diagram for the given situation in the question.
b. Conserving energy between "O" and "A"
`U_i + K_i = U_f + K_f`
⇒ `0 + 1/2 mv^2 = mgh + 1/2 mv^'`
⇒ `(v^')^2/2 = v^2/2 = - gh`
⇒ `(v^')^2 = v^2 - 2 gh`
⇒ `v^' = sqrt(v^2 - 2 gh)` ......(i)
Where v' is the speed of the bullet just before hitting the target. Let speed after emerging from the target is v" then,
By question, = `1/2 (mv^")^2 = 1/2[1/2 m(v^')^2]`
= `1/2 m(v^")^2`
= `1/4 m(v^')^2`
= `1/4 m[v^2 - 2 gh]`
⇒ `(v^")^2 = (v^2 - 2 gh)/2 = v^2/2 - gh`
⇒ `v^" = sqrt(v^2/2 - gh)` .....(ii)
From equations (i) and (ii)
`v^'/v^" = (sqrt(v^2 - 2 gh))/(sqrt(v^2 - 2 gh)/(sqrt(2))) = sqrt(2)`
⇒ `v^" = v^'/sqrt(2) = v^2 (v^'/2)`
⇒ `v^"/(v^'/2) = sqrt(2)` = 1.414 > 1
⇒ `v^" > v^'/2`
Hence, after emerging from the target velocity of the bullet (v") is more than half of its earlier velocity v’ (velocity before emerging into the target).
d. As the velocity of the bullet changes to v’ which is less than v1 hence, the path, followed will change and the bullet reaches point B instead of A', as shown in the figure.
f. As the bullet is passing through the target the loss in energy of the bullet is transferred to particles of the target. Therefore, their internal energy increases.
APPEARS IN
RELATED QUESTIONS
In figure (i) the man walks 2 m carrying a mass of 15 kg on his hands. In Figure (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
Is work-energy theorem valid in non-inertial frames?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. what are the initial and final kinetic energies of the ball?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. What is the work done by the kinetic friction?
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. Assuming that the track, wind etc. offered an average resistance of one-tenth of her weight, calculate the work done by the resistance during the run.
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. What power Griffith-Joyner had to exert to maintain uniform speed?
A block of mass 30 kg is being brought down by a chain. If the block acquires a speed of 40 cm/s in dropping down 2 m, find the work done by the chain during the process.
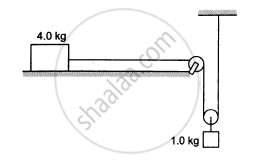
Consider the situation shown in the following figure. The system is released from rest and the block of mass 1 kg is found to have a speed 0⋅3 m/s after it has descended a distance of 1 m. Find the coefficient of kinetic friction between the block and the table.
A block of mass 100 g is moved with a speed of 5⋅0 m/s at the highest point in a closed circular tube of radius 10 cm kept in a vertical plane. The cross-section of the tube is such that the block just fits in it. The block makes several oscillations inside the tube and finally stops at the lowest point. Find the work done by the tube on the block during the process.
A heavy particle is suspended by a 1⋅5 m long string. It is given a horizontal velocity of \[\sqrt{57} \text{m/s}\] (a) Find the angle made by the string with the upward vertical when it becomes slack. (b) Find the speed of the particle at this instant. (c) Find the maximum height reached by the particle over the point of suspension. Take g = 10 m/s2.
A particle of mass m is kept on the top of a smooth sphere of radius R. It is given a sharp impulse which imparts it a horizontal speed ν. (a) Find the normal force between the sphere and the particle just after the impulse. (b) What should be the minimum value of ν for which the particle does not slip on the sphere? (c) Assuming the velocity ν to be half the minimum calculated in part, (b) find the angle made by the radius through the particle with the vertical when it leaves the sphere.
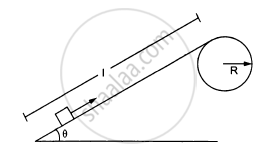
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. Find the minimum projection-speed \[\nu_0\] for which the particle reaches the top of the track.
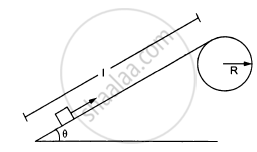
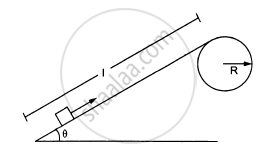
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom.Assuming that the projection-speed is only slightly greater than \[\nu_0\] , where will the block lose contact with the track?
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Find the tangential acceleration \[\frac{d\nu}{dt}\] of the chain when the chain starts sliding down.
A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 ms–1. Calculate
- the loss of P.E. of the drop.
- the gain in K.E. of the drop.
- Is the gain in K.E. equal to a loss of P.E.? If not why.
Take g = 10 ms–2
Suppose the average mass of raindrops is 3.0 × 10–5 kg and their average terminal velocity 9 ms–1. Calculate the energy transferred by rain to each square metre of the surface at a place which receives 100 cm of rain in a year.
A rocket accelerates straight up by ejecting gas downwards. In a small time interval ∆t, it ejects a gas of mass ∆m at a relative speed u. Calculate KE of the entire system at t + ∆t and t and show that the device that ejects gas does work = `(1/2)∆m u^2` in this time interval (neglect gravity).
