Advertisements
Advertisements
Question
Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. Assuming that the projection-speed is \[\nu_0\] and that the block does not lose contact with the track before reaching its top, find the force acting on it when it reaches the top.
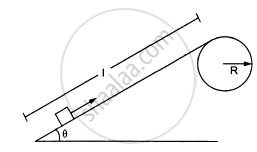
Solution
(b) When the block is projected at a speed:
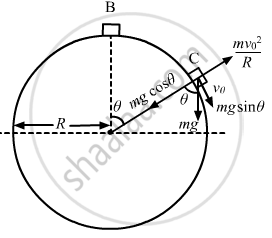
Let the velocity at C be \[\nu_0\] .
Applying energy principle,
\[\left( \frac{1}{2} \right) \text{m}\nu_0^2 - \left( \frac{1}{2} \right) \text{m}\left( 2 \nu_0 \right)^2 \]
\[ = - \text{mg} \left[ \text{ l } \sin \theta + R \left( 1 - \cos \theta \right) \right]\]
\[ \Rightarrow V^2 = 4 \nu_0^2 - 2g \left[ \text{ l } \sin g \theta + R \left( 1 - \cos \theta \right) \right]\]
\[ = 4 . 2 g \left[ \text{ l } \sin \theta + R \left( 1 - \cos \theta \right) \right] - \]
\[2g \left[ \text{ l } \sin \theta + R \left( 1 - \cos \theta \right) \right]\]
So, force acting on the body,
APPEARS IN
RELATED QUESTIONS
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. What is the work done by the kinetic friction?
Consider the situation of the previous question from a frame moving with a speed v0 parallel to the initial velocity of the block. (a) What are the initial and final kinetic energies? (b) What is the work done by the kinetic friction?
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. Assuming that the track, wind etc. offered an average resistance of one-tenth of her weight, calculate the work done by the resistance during the run.
An unruly demonstrator lifts a stone of mass 200 g from the ground and throws it at his opponent. At the time of projection, the stone is 150 cm above the ground and has a speed of 3 m/s. Calculate the work done by the demonstrator during the process. If it takes one second for the demonstrator to lift the stone and throw it, what horsepower does he use?
A scooter company gives the following specifications about its product:
Weight of the scooter − 95 kg
Maximum speed − 60 km/h
Maximum engine power − 3⋅5 hp
Pick up time to get the maximum speed − 5 s
Check the validity of these specifications.
A block of mass 30 kg is being brought down by a chain. If the block acquires a speed of 40 cm/s in dropping down 2 m, find the work done by the chain during the process.
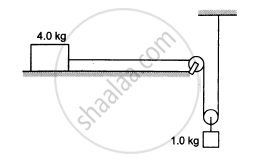
Consider the situation shown in the following figure. The system is released from rest and the block of mass 1 kg is found to have a speed 0⋅3 m/s after it has descended a distance of 1 m. Find the coefficient of kinetic friction between the block and the table.
A block of mass 5 kg is suspended from the end of a vertical spring which is stretched by 10 cm under the load of the block. The block is given a sharp impulse from below, so that it acquires an upward speed of 2 m/s. How high will it rise? Take g = 10 m/s2.
A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed 10 cm shorter than its natural length and the system is released from this position. How high does the block rise ? Take g = 10 m/s2.
Following figure following shows a smooth track, a part of which is a circle of radius R. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

A heavy particle is suspended by a 1⋅5 m long string. It is given a horizontal velocity of \[\sqrt{57} \text{m/s}\] (a) Find the angle made by the string with the upward vertical when it becomes slack. (b) Find the speed of the particle at this instant. (c) Find the maximum height reached by the particle over the point of suspension. Take g = 10 m/s2.
A particle of mass m is kept on the top of a smooth sphere of radius R. It is given a sharp impulse which imparts it a horizontal speed ν. (a) Find the normal force between the sphere and the particle just after the impulse. (b) What should be the minimum value of ν for which the particle does not slip on the sphere? (c) Assuming the velocity ν to be half the minimum calculated in part, (b) find the angle made by the radius through the particle with the vertical when it leaves the sphere.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
A smooth sphere of radius R is made to translate in a straight line with a constant acceleration a. A particle kept on the top of the sphere is released at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle θ it slides.
An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because ______.
A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
- Work done by all forces on man is equal to the rise in potential energy mgL.
- Work done by all forces on man is zero.
- Work done by the gravitational force on man is mgL.
- The reaction force from a step does not do work because the point of application of the force does not move while the force exists.
Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare?
A rocket accelerates straight up by ejecting gas downwards. In a small time interval ∆t, it ejects a gas of mass ∆m at a relative speed u. Calculate KE of the entire system at t + ∆t and t and show that the device that ejects gas does work = `(1/2)∆m u^2` in this time interval (neglect gravity).
