Advertisements
Advertisements
Question
Consider the situation shown in the following figure. The system is released from rest and the block of mass 1 kg is found to have a speed 0⋅3 m/s after it has descended a distance of 1 m. Find the coefficient of kinetic friction between the block and the table.
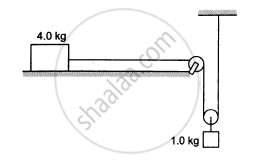
Solution
\[\text{Given}, \]
\[ \text{m}_1 = 4 \text{ kg, m}_2 = 1 \text{kg } , \]
\[ \text{v}_2 = 0 . 3 \text{ m/s}\]
\[ \text{v}_1 = 2 \times 0 . 3 = 0 . 6 \text{ m/s}\]
\[\left( \text{ v}_1 = 2 \text{ v}_2 \text{ in this system } \right)\]
\[\text{ Height descended by the 1 kg block, h = 1 m } \]
\[\text{ Distance travelled by the 4 kg block } , \]
\[\text{ s } = 2 \times 1 = 2 \text{ m }\]
\[\text{ Initially the system is at rest . So, u }= 0\]
\[\text{ Applying work energy theoremwhich says that } \]
\[\text{ change in K . E . = Work done } \left( \text{ for the system } \right)\]
\[\left( \frac{1}{2} \right) \text{m}_1 \nu_1^2 + \left( \frac{1}{2} \right) \text{m}_2 \nu_2^2 = \left( - \mu \text{ R } \right) \text{ s } + \text{m}_2 \text{gh}\]
\[\frac{1}{2} \times 4 \times \left( 0 . 36 \right) + \frac{1}{2} \times 1 \times \left( 0 . 09 \right) [\text{ As, R = 4g = 40 N} ]\]
\[ = - \mu 40 \times 2 + 1 \times 40 \times 1\]
\[ \Rightarrow 0 . 72 + 0 . 045 = - 80 \mu + 10\]
\[ \Rightarrow \mu = \frac{9 . 235}{80} = 0 . 12\]
So, the coefficient of kinetic friction between the block and the table is 0.12 .
APPEARS IN
RELATED QUESTIONS
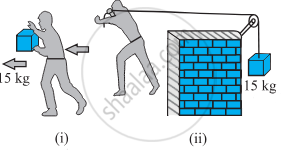
In Figure (i) the man walks 2 m carrying a mass of 15 kg on his hands. In Figure (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
Is work-energy theorem valid in non-inertial frames?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. what are the initial and final kinetic energies of the ball?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. What is the work done by the kinetic friction?
Consider the situation of the previous question from a frame moving with a speed v0 parallel to the initial velocity of the block. (a) What are the initial and final kinetic energies? (b) What is the work done by the kinetic friction?
In a factory, 2000 kg of metal needs to be lifted by an engine through a distance of 12 m in 1 minute. Find the minimum horsepower of the engine to be used.
A scooter company gives the following specifications about its product:
Weight of the scooter − 95 kg
Maximum speed − 60 km/h
Maximum engine power − 3⋅5 hp
Pick up time to get the maximum speed − 5 s
Check the validity of these specifications.
A small block of mass 200 g is kept at the top of a frictionless incline which is 10 m long and 3⋅2 m high. How much work was required (a) to lift the block from the ground and put it an the top, (b) to slide the block up the incline? What will be the speed of the block when it reaches the ground if (c) it falls off the incline and drops vertically to the ground (d) it slides down the incline? Take g = 10 m/s2.
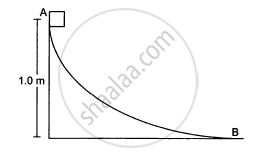
A block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (In the following figure). The rough surface has a friction coefficient of 0⋅20 with the block. If the block starts slipping on the track from a point 1⋅0 m above the horizontal surface, how far will it move on the rough surface?
A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The spring is now compressed 10 cm shorter than its natural length and the system is released from this position. How high does the block rise ? Take g = 10 m/s2.
Following figure following shows a smooth track, a part of which is a circle of radius R. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

The bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of \[\sqrt{3 gl}\] . Find the angle rotated by the string before it becomes slack.
A heavy particle is suspended by a 1⋅5 m long string. It is given a horizontal velocity of \[\sqrt{57} \text{m/s}\] (a) Find the angle made by the string with the upward vertical when it becomes slack. (b) Find the speed of the particle at this instant. (c) Find the maximum height reached by the particle over the point of suspension. Take g = 10 m/s2.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Find the gravitational potential energy of the chain with reference level at the centre of the sphere.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
A bullet of mass m fired at 30° to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of bullet after it emerges out of the target?
- The velocity of the bullet will be reduced to half its initial value.
- The velocity of the bullet will be more than half of its earlier velocity.
- The bullet will continue to move along the same parabolic path.
- The bullet will move in a different parabolic path.
- The bullet will fall vertically downward after hitting the target.
- The internal energy of the particles of the target will increase.
Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of same magnitude. How would the distance moved by them before coming to rest compare?
A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 ms–1. Calculate
- the loss of P.E. of the drop.
- the gain in K.E. of the drop.
- Is the gain in K.E. equal to a loss of P.E.? If not why.
Take g = 10 ms–2
Suppose the average mass of raindrops is 3.0 × 10–5 kg and their average terminal velocity 9 ms–1. Calculate the energy transferred by rain to each square metre of the surface at a place which receives 100 cm of rain in a year.
A rocket accelerates straight up by ejecting gas downwards. In a small time interval ∆t, it ejects a gas of mass ∆m at a relative speed u. Calculate KE of the entire system at t + ∆t and t and show that the device that ejects gas does work = `(1/2)∆m u^2` in this time interval (neglect gravity).
