Advertisements
Advertisements
प्रश्न
Two blocks M1 and M2 having equal mass are free to move on a horizontal frictionless surface. M2 is attached to a massless spring as shown in figure. Iniially M2 is at rest and M1 is moving toward M2 with speed v and collides head-on with M2.
- While spring is fully compressed all the KE of M1 is stored as PE of spring.
- While spring is fully compressed the system momentum is not conserved, though final momentum is equal to initial momentum.
- If spring is massless, the final state of the M1 is state of rest.
- If the surface on which blocks are moving has friction, then collision cannot be elastic.
Advertisements
उत्तर
c and d
Explanation:
If it is not specified we always consider the collision elastic.
When two bodies of equal masses collide elastically, their velocities are interchanged in these types of collision.
Kinetic energy and linear momentum remain conserved.
According to the above diagram when m1 comes in contact with the spring, m1 is retarded by the spring force and m2 is accelerated by the spring force.
- The spring will continue to compress until the two blocks acquire a common velocity. So some of the kinetic energy of block Mx is stored in P.E and some part of it stores in K.E of block M2. So option (a) is incorrect.
- As surfaces are frictionless momentum of the system will be conserved. So option (b) is also incorrect.
- The two bodies of equal mass exchange their velocities in a head-on elastic collision between them. So, if spring is massless, the final state of the M1 is a state of rest.
- Since there is a loss of K.E when the blocks collide on the rough surface. Hence, the collision is inelastic.
APPEARS IN
संबंधित प्रश्न
State if the following statement is true or false. Give a reason for your answer.
In an elastic collision of two bodies, the momentum and energy of each body is conserved.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figure is a possible result after collision?
A bullet of mass 0.012 kg and horizontal speed 70 m s–1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Solve the following problem.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce, 64% of the potential energy is converted into kinetic energy. Calculate the following:
- Coefficient of restitution.
- The speed with which the ball comes up from the ground after the third bounce.
- The impulse was given by the ball to the ground during this bounce.
- Average force exerted by the ground if this impact lasts for 250 ms.
- The average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm2.
Define the following:
Coefficient of restitution
A ball is thrown vertically down from height of 80 m from the ground with an initial velocity 'v'. The ball hits the ground, loses `1/6`th of its total mechanical energy, and rebounds back to the same height. If the acceleration due to gravity is 10 ms-2, the value of 'v' is
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
A mass M moving with velocity 'v' along x-axis collides and sticks to another mass 2M which is moving along Y-axis with velocity 3v. After collision, the velocity of the combination is ______.
A body of mas 'm' moving with speed 3 m/s collides with a body of mass '2m' at rest. The coalesced mass will start to move with a speed of ______.
During inelastic collision between two bodies, which of the following quantities always remain conserved?
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
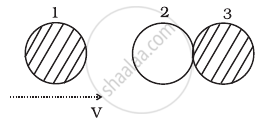
If the collision is elastic, which of the following (Figure) is a possible result after collision?
A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for 0.001s, the force that the batsman had to apply to hold the bat firmly at its place would be ______.
A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that for head-on collision, both the balls move forward.
A ball of mass m, moving with a speed 2v0, collides inelastically (e > 0) with an identical ball at rest. Show that for a general collision, the angle between the two velocities of scattered balls is less than 90°.
A ball falls from a height of 1 m on a ground and it loses half its kinetic energy when it hits the ground. What would be the total distance covered by the ball after sufficiently long time?
An alpha-particle of mass m suffers 1-dimensional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing, 64% of its initial kinetic energy. The mass of the nucleus is ______.
The dimension of mutual inductance is ______.
In a collision, what type of interaction occurs between objects?
Before collision, what is the position of objects?
