Advertisements
Advertisements
प्रश्न
Consider the decay of a free neutron at rest : n → p + e–
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus

उत्तर १
The decay process of free neutron at rest is given as:
n → p + e–
From Einstein’s mass-energy relation, we have the energy of electron as Δmc2
Where,
Δm = Mass defect = Mass of neutron – (Mass of proton + Mass of electron)
c = Speed of light
Δm and c are constants. Hence, the given two-body decay is unable to explain the continuous energy distribution in the β-decay of a neutron or a nucleus. The presence of neutrino νon the LHS of the decay correctly explains the continuous energy distribution.
उत्तर २
Let the masses of the electron and proton be m and M respectively. Let v and V be the velocities of electron and proton respectively. Using law of conservation of momentum. Momentum of electron + momentum of proton = momentum of neutron
`:. mv + MV = 0 => V = - m/M v`
Clearly the electron and the proton move in opposite directions. If mass `trianglem` has been conveted into energy in the reaction then
`1/2mv^2 + 1/2 MV^2 = trianglem xx c^2`
or `1/2mv^2 + 1/2M[-m/M]^2v^2 = trianglemc^2`
or `1/2mv^2[1+m/M] = trianglemc^2`
or `v^2 = (2Mtrianglemc^2)/(m(M+m))`
Thus, it is proved that the value of v2 is fixed since all the quantities in right hand side are constant. It establishes that the emitted electron must have a fixed energy and thus we cannot account for the continuous energy distribution in the β-decay of a neutron.
APPEARS IN
संबंधित प्रश्न
Answer carefully, with reason:
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
Define coefficient of restitution.
Solve the following problem.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce, 64% of the potential energy is converted into kinetic energy. Calculate the following:
- Coefficient of restitution.
- The speed with which the ball comes up from the ground after the third bounce.
- The impulse was given by the ball to the ground during this bounce.
- Average force exerted by the ground if this impact lasts for 250 ms.
- The average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm2.
Solve the following problem.
A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of mass ratio 1:2. The lighter fragment continues to travel downwards with a speed of 60 m/s. Calculate the kinetic energy supplied during the explosion.
Arrive at an expression for elastic collision in one dimension and discuss various cases.
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
In an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls (i.e., when they are in contact).
- Kinetic energy.
- Total linear momentum?
Give reason for your answer in each case.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
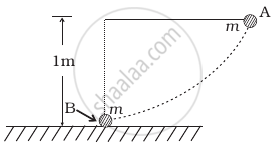
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
A particle of mass m with an initial velocity u`hat"i"` collides perfectly elastically with a mass 3m at rest. It moves with a velocity v`hat"j"` after collision, then, v is given by :
A ball is thrown upwards from the foot of a tower. The ball crosses the top of tower twice after an interval of 4 seconds and the ball reaches ground after 8 seconds, then the height of tower is ______ m. (g = 10 m/s2)
