Advertisements
Advertisements
Question
Consider the decay of a free neutron at rest : n → p + e–
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus

Solution 1
The decay process of free neutron at rest is given as:
n → p + e–
From Einstein’s mass-energy relation, we have the energy of electron as Δmc2
Where,
Δm = Mass defect = Mass of neutron – (Mass of proton + Mass of electron)
c = Speed of light
Δm and c are constants. Hence, the given two-body decay is unable to explain the continuous energy distribution in the β-decay of a neutron or a nucleus. The presence of neutrino νon the LHS of the decay correctly explains the continuous energy distribution.
Solution 2
Let the masses of the electron and proton be m and M respectively. Let v and V be the velocities of electron and proton respectively. Using law of conservation of momentum. Momentum of electron + momentum of proton = momentum of neutron
`:. mv + MV = 0 => V = - m/M v`
Clearly the electron and the proton move in opposite directions. If mass `trianglem` has been conveted into energy in the reaction then
`1/2mv^2 + 1/2 MV^2 = trianglem xx c^2`
or `1/2mv^2 + 1/2M[-m/M]^2v^2 = trianglemc^2`
or `1/2mv^2[1+m/M] = trianglemc^2`
or `v^2 = (2Mtrianglemc^2)/(m(M+m))`
Thus, it is proved that the value of v2 is fixed since all the quantities in right hand side are constant. It establishes that the emitted electron must have a fixed energy and thus we cannot account for the continuous energy distribution in the β-decay of a neutron.
APPEARS IN
RELATED QUESTIONS
Answer carefully, with reason:
In an inelastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact)?
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figure is a possible result after collision?

The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table, as shown in the figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Which of the following potential energy curves in Fig. cannot possibly describe the elastic collision of two billiard balls? Here r is distance between centres of the balls.

Define the following:
Coefficient of restitution
In inelastic collision, ____________.
A wooden block of mass 'M' moves with velocity 'v ' and collides with another block of mass '4M' which is at rest. After collision, the block of mass 'M' comes to rest. The coefficient of restitution will be ______.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
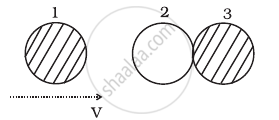
If the collision is elastic, which of the following (Figure) is a possible result after collision?
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
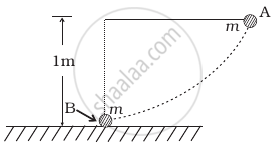
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and required 1 s to cover. How long the drunkard takes to fall in a pit 13 m away from the start?
