Advertisements
Advertisements
Question
The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table, as shown in the figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Solution
When the bob A of a pendulum, released from an angle of 30° to the vertical, collides with another stationary bob B of the the same mass, the collision being elastic, their velocities are exchanged. As a result of this elastic collision, bob A will come to rest immediately after the impact, while bob B will acquire the velocity that bob A had just before the collision. Therefore, after the collision, bob A does not rise again; it remains at rest
APPEARS IN
RELATED QUESTIONS
A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 m s–1 relative to the trolley in a direction opposite to the its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
Answer the following question.
A bullet of mass m1 travelling with a velocity u strikes a stationary wooden block of mass m2 and gets embedded into it. Determine the expression for loss in the kinetic energy of the system. Is this violating the principle of conservation of energy? If not, how can you account for this loss?
In Rutherford experiment, for head-on collision of a-particles with a gold nucleus, the impact parameter is ______.
In inelastic collision, ____________.
A body of mas 'm' moving with speed 3 m/s collides with a body of mass '2m' at rest. The coalesced mass will start to move with a speed of ______.
A smooth sphere of mass 'M' moving with velocity 'u' directly collides elastically with another sphere of mass 'm' at rest. After collision, their final velocities are V' and V respectively. The value of V is given by ______.
Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D in which the relation between potential energy V, kinetic energy (K) and total energy E is as given below:
Region A : V > E
Region B : V < E
Region C : K > E
Region D : V > K
State with reason in each case whether a particle can be found in the given region or not.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
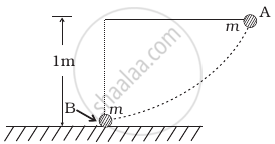
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
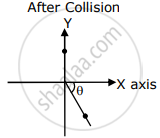
A ball of mass 10 kg moving with a velocity of 10`sqrt3` ms–1 along the X-axis, hits another ball of mass 20 kg which is at rest. After collision, the first ball comes to rest and the second one disintegrates into two equal pieces. One of the pieces starts moving along Y-axis at a speed of 10 m/s. The second piece starts moving at a speed of 20 m/s at an angle θ (degree) with respect to the X-axis.
The configuration of pieces after the collision is shown in the figure.
The value of θ to the nearest integer is ______.
Three identical blocks A, B and C are placed on horizontal frictionless surface. The blocks A and C are at rest. But A is approaching towards B with a speed 10 m/s. The coefficient of restitution for all collision is 0.5. The speed of the block C just after the collision is ______.

