Advertisements
Advertisements
Question
Answer the following question.
A bullet of mass m1 travelling with a velocity u strikes a stationary wooden block of mass m2 and gets embedded into it. Determine the expression for loss in the kinetic energy of the system. Is this violating the principle of conservation of energy? If not, how can you account for this loss?
Solution
- A bullet of mass m1 travelling with a velocity u, striking a stationary wooden block of mass m2 and getting embedded into it is a case of perfectly inelastic collision.
- In a perfectly inelastic collision, although there is a loss in kinetic energy, the principle of conservation of energy is not violated as the total energy of the system is conserved.
Loss in the kinetic energy during a perfectly inelastic head-on collision:
- Let two bodies A and B of masses m1 and m2 moving with initial velocity `vec"u"_1 and vec"u"_2` respectively such that particle A collides headon with particle B i.e., `"u"_1 > "u"_2`.
- If the collision is perfectly inelastic, the particles stick together and move with a common velocity `vec"v"` after the collision along the same straight line.
loss in kinetic energy = total initial
kinetic energy – total final kinetic energy, - By the law of conservation of momentum, m1u1 + m2 u2 = (m1 + m2) v
∴ v = `("m"_1"u"_1 + "m"_2"u"_2)/("m"_1 + "m"_2)` - Loss of kinetic energy,
`Delta "K.E" = (1/2"m"_1"u"_1^2 + 1/2"m"_2"u"_2^2) - 1/2("m"_1 + "m"_2)"v"^2`
`= (1/2"m"_1"u"_1^2 + 1/2"m"_2"u"_2^2) -1/2("m"_1 + "m"_2)[("m"_1"u"_1 + "m"_2"u"_2)/("m"_1 + "m"_2)]^2`
`= ("m"_1^2"u"_1^2 + "m"_1"m"_2"u"_2^2 + "m"_1"m"_2"u"_1^2)/(2("m"_1 + "m"_2)) + ("m"_2^2 "u"_2^2 - "m"_1^2"u"_1^2 - "m"_2^2"u"_2^2 - 2"m"_1"m"_2"u"_1"u"_2)/(2("m"_1 + "m"_2))`
`= ("m"_1"m"_2)/(2("m"_1 + "m"_2)) ("u"_1 - "u"_2)^2` - Both the masses and the term `("u"_1 - "u"_2)^2` are positive. Hence, there is always a loss in a perfectly inelastic collision. For a perfectly inelastic collision, as e = 0, the loss is maximum.
APPEARS IN
RELATED QUESTIONS
In an inelastic collision of two bodies, the quantities which do not change after the collision are the ______ of the system of two bodies.
State if the following statement is true or false. Give a reason for your answer.
In an elastic collision of two bodies, the momentum and energy of each body is conserved.
A molecule in a gas container hits a horizontal wall with speed 200 m s–1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figure is a possible result after collision?

The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table, as shown in the figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 m s–1 relative to the trolley in a direction opposite to the its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
Consider the decay of a free neutron at rest : n → p + e–
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus

Explain the characteristics of elastic and inelastic collision.
Define the following:
Coefficient of restitution
Arrive at an expression for elastic collision in one dimension and discuss various cases.
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
In inelastic collision, ____________.
A wooden block of mass 'M' moves with velocity 'v ' and collides with another block of mass '4M' which is at rest. After collision, the block of mass 'M' comes to rest. The coefficient of restitution will be ______.
Two bodies of masses 3 kg and 2 kg collide bead-on. Their relative velocities before and after collision are 20 m/s and 5 m/s respectively. The loss of kinetic energy of the system is ______.
A body of mas 'm' moving with speed 3 m/s collides with a body of mass '2m' at rest. The coalesced mass will start to move with a speed of ______.
A smooth sphere of mass 'M' moving with velocity 'u' directly collides elastically with another sphere of mass 'm' at rest. After collision, their final velocities are V' and V respectively. The value of V is given by ______.
A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for 0.001s, the force that the batsman had to apply to hold the bat firmly at its place would be ______.
Two blocks M1 and M2 having equal mass are free to move on a horizontal frictionless surface. M2 is attached to a massless spring as shown in figure. Iniially M2 is at rest and M1 is moving toward M2 with speed v and collides head-on with M2.

- While spring is fully compressed all the KE of M1 is stored as PE of spring.
- While spring is fully compressed the system momentum is not conserved, though final momentum is equal to initial momentum.
- If spring is massless, the final state of the M1 is state of rest.
- If the surface on which blocks are moving has friction, then collision cannot be elastic.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
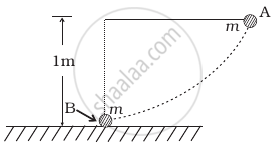
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses `(m/M)` is `1/x`. The value of 'x' will be ______.
A ball of mass 10 kg moving with a velocity of 10`sqrt3` ms–1 along the X-axis, hits another ball of mass 20 kg which is at rest. After collision, the first ball comes to rest and the second one disintegrates into two equal pieces. One of the pieces starts moving along Y-axis at a speed of 10 m/s. The second piece starts moving at a speed of 20 m/s at an angle θ (degree) with respect to the X-axis.
The configuration of pieces after the collision is shown in the figure.
The value of θ to the nearest integer is ______.
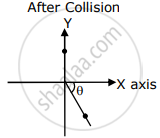
A particle of mass m with an initial velocity u`hat"i"` collides perfectly elastically with a mass 3m at rest. It moves with a velocity v`hat"j"` after collision, then, v is given by :
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and required 1 s to cover. How long the drunkard takes to fall in a pit 13 m away from the start?
A ball falls from a height of 1 m on a ground and it loses half its kinetic energy when it hits the ground. What would be the total distance covered by the ball after sufficiently long time?
A sphere of mass 'm' moving with velocity 'v' collides head-on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is ______. ( e is coefficient of restitution and collision is inelastic)
Three identical blocks A, B and C are placed on horizontal frictionless surface. The blocks A and C are at rest. But A is approaching towards B with a speed 10 m/s. The coefficient of restitution for all collision is 0.5. The speed of the block C just after the collision is ______.

