Advertisements
Advertisements
Question
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
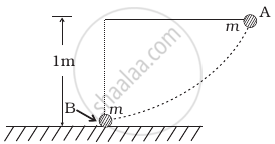
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
Solution
a. Two balls have the same mass and the collision between them is elastic, therefore, ball A transfers its entire linear momentum to ball 8. Hence, ball A will come to rest after the collision and does not rise at all.
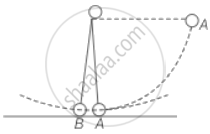
b. Speed with which bob B starts moving
= Speed with which bob A hits bob B
= `sqrt(2gh)`
= `sqrt(2 xx 9.8 xx 1)`
= `sqrt(19.6)`
= 4.42 m/s
APPEARS IN
RELATED QUESTIONS
Answer carefully, with reason:
If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy.)
A bullet of mass 0.012 kg and horizontal speed 70 m s–1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
A particle of mass 'm' collides with another stationary particle of mass 'M'. A particle of mass 'm' stops just after collision. The coefficient of restitution is ______.
A block of mass 'm' moving along a straight line with constant velocity `3vec"v"` collides with another block of same mass at rest. They stick together and move with common velocity. The common velocity is ______.
Two bodies of masses 3 kg and 2 kg collide bead-on. Their relative velocities before and after collision are 20 m/s and 5 m/s respectively. The loss of kinetic energy of the system is ______.
A rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses `(m/M)` is `1/x`. The value of 'x' will be ______.
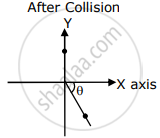
A ball of mass 10 kg moving with a velocity of 10`sqrt3` ms–1 along the X-axis, hits another ball of mass 20 kg which is at rest. After collision, the first ball comes to rest and the second one disintegrates into two equal pieces. One of the pieces starts moving along Y-axis at a speed of 10 m/s. The second piece starts moving at a speed of 20 m/s at an angle θ (degree) with respect to the X-axis.
The configuration of pieces after the collision is shown in the figure.
The value of θ to the nearest integer is ______.
A particle of mass m with an initial velocity u`hat"i"` collides perfectly elastically with a mass 3m at rest. It moves with a velocity v`hat"j"` after collision, then, v is given by :
An insect moves with a constant velocity v from one corner of a room to other corner which is opposite of the first corner along the largest diagonal of room. If the insect can not fly and dimensions of room is a × a × a, then the minimum time in which the insect can move is `"a"/"v"`. times the square root of a number n, then n is equal to ______.
A sphere of mass 'm' moving with velocity 'v' collides head-on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is ______. ( e is coefficient of restitution and collision is inelastic)
