Advertisements
Advertisements
प्रश्न
A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 m s–1 relative to the trolley in a direction opposite to the its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
उत्तर १
Mass of the trolley, M = 200 kg
Speed of the trolley, v = 36 km/h = 10 m/s
Mass of the boy, m = 20 kg
Initial momentum of the system of the boy and the trolley
= (M + m)v
= (200 + 20) × 10
= 2200 kg m/s
Let v' be the final velocity of the trolley with respect to the ground.
Final velocity of the boy with respect to the ground = v' - 4
Final momentum = Mv' + m(v' - 4)
= 200v' + 20v' - 80
= 220v' – 80
As per the law of conservation of momentum:
Initial momentum = Final momentum
2200 = 220v' – 80
∴ v' = 2280 / 220 = 10.36 m/s
Length of the trolley, l = 10 m
Speed of the boy, v'' = 4 m/s
Time taken by the boy to run, t = 10/4 = 2.5 s
∴ Distance moved by the trolley = v'' × t= 10.36 × 2.5 = 25.9 m
उत्तर २
Let there be an observer travelling parallel to the trolley with the same speed. He will observe the initial momentum of the trolley of mass M and child of mass m as zero. When the child jumps in opposite direction, he will observe the increase in the velocity of the trolley by Δv.
Let u be the velocity of the child. He will observe child landing at velocity (u – Δu) Therefore, initial momentum = 0
Final momentum = MΔ v – m (u – Δv)
Hence, MΔ v – m (u – Δv) = 0
Whence Δv =mu/ M + m
Putting values Δv =4 x 20/ 20 + 220 = ms-1
∴ Final speed of trolley is 10.36 ms-1.
The child take 2.5 s to run on the trolley.
Therefore, the trolley moves a distance = 2.5 x 10.36 m = 25.9 m.
APPEARS IN
संबंधित प्रश्न
Answer carefully, with reason:
In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figure is a possible result after collision?

Solve the following problem.
A marble of mass 2m travelling at 6 cm/s is directly followed by another marble of mass m with double speed. After a collision, the heavier one travels with the average initial speed of the two. Calculate the coefficient of restitution.
Arrive at an expression for elastic collision in one dimension and discuss various cases.
A mass M moving with velocity 'v' along x-axis collides and sticks to another mass 2M which is moving along Y-axis with velocity 3v. After collision, the velocity of the combination is ______.
A body of mas 'm' moving with speed 3 m/s collides with a body of mass '2m' at rest. The coalesced mass will start to move with a speed of ______.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
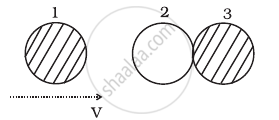
If the collision is elastic, which of the following (Figure) is a possible result after collision?
Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D in which the relation between potential energy V, kinetic energy (K) and total energy E is as given below:
Region A : V > E
Region B : V < E
Region C : K > E
Region D : V > K
State with reason in each case whether a particle can be found in the given region or not.
An alpha-particle of mass m suffers 1-dimensional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing, 64% of its initial kinetic energy. The mass of the nucleus is ______.
The dimension of mutual inductance is ______.
