हिंदी
CISCEISC (Science) ISC Class 11
प्रश्न पत्र१७
अवधारणा स्पष्टीकरण और वीडियो१६४
पाठ्यक्रम

Potential Energy of a Spring

Advertisements

Topics

Notes

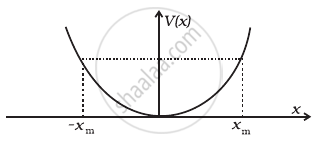
Potential energy of spring

  • The spring force is an example of a variable force, which is conservative.

  • In an ideal spring, Fs = − kx , this force law for the spring is called Hooke’s law.

  • The constant k is called the spring constant. Its unit is N m-1.

  • The spring is said to be stiff if k is large and soft if k is small.


Spring force is position dependent as first stated by Hooke,
Fs = − kx

  • Work done by spring force only depends on the initial and final positions. Thus, the spring force is a conservative force.

  • We define the potential energy V(x) of the spring to be zero when block and spring system is in the equilibrium position.

  • If the extension is xm, the work done by the spring force is

`W_s = ∫_0^(x_m) F_s  dx=-∫_0^(x_m) kx  dx`
     `=-(kx_m^2)/2`
The same is true when the spring is compressed with a displacement xc (< 0). The spring force does work Ws = -kx2/2 while the external force F does work + kxc^2/2. If the block is moved from an initial displacement xi to a final displacement xf, the work done by the spring force Ws is

`W_s = -∫_(x_i)^(x_f) kx  dx = (kx_i^2)/2 - (kx_f^2)/2`
Thus the work done by the spring force depends only on the end points. Specifically, if the block is pulled from xi and allowed to return to xi;
`W_s = -∫_(x_i)^(x_f) kx  dx = (kx_i^2)/2 - (kx_f^2)/2 = 0`
The work done by the spring force in a cyclic process is zero.

We have explicitly demonstrated that the spring force
(i) is position dependent only as first stated by Hooke, (Fs = − kx);
(ii) does work which only depends on the initial and final positions.
Thus, the spring force is a conservative force.

We define the potential energy V(x) of the spring to be zero when block and spring system is in the equilibrium position. For an extension (or compression) x the above analysis suggests that
`V(x)=(kx^2)/2`

If the block of mass m is extended to xm and released from rest, then its total mechanical energy at any arbitrary point x (where x lies between – xm and + xm) will be given by:
`1/2 kx_m^2 = 1/2 kx^2 + 1/2 mv^2`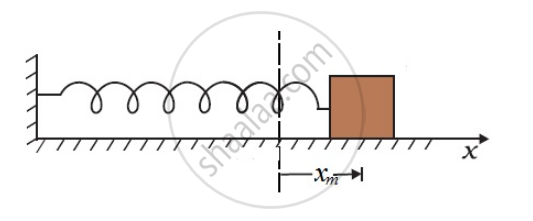
This suggests that the speed and the kinetic energy will be maximum at the equilibrium position, x = 0, i.e.,
`1/2 mv_m^2 = 1/2 kx_m^2`
where vm is the maximum speed.
Or `v_m= sqrt(k/m)  x_m`

Note that k/m has the dimensions of `[T^(-2)]` and our equation is dimensionally correct.
The kinetic energy gets converted to potential energy and vice versa, however, the total mechanical energy remains constant. This is graphically depicted in Fig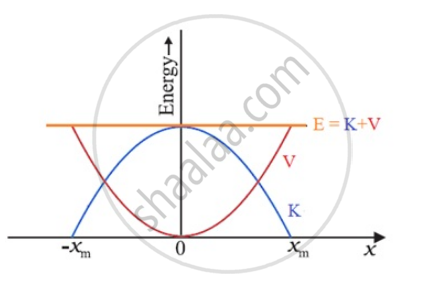

Example: A car of mass M travelling with speed v, collides with a spring, having spring constant k. The car comes to rest (momentarily) when spring is compressed to a distance of `x_m`. Find `x_m`
Solution: Work done on car = `K_f-K_i=0-(mv^2)/2 =-(mv^2)/2`
Work done by spring, `W_s= -∫_(x_i)^(x_f) kx  dx =-∫_(0)^(x_m) kx  dx = -(kx_m^2)/2`
Now work done by spring equals work done on car => `-(mv^2)/2 = - (kx_m^2)/2` 
`x_m = sqrt (m/k)  v`

If you would like to contribute notes or other learning material, please submit them using the button below.

Related QuestionsVIEW ALL [17]

The potential energy function for a particle executing linear simple harmonic motion is given by V(x) =`(kx^2)/2`, where k is the force constant of the oscillator. For k = 0.5 N m–1, the graph of V(x) versus x is shown in the figure. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.

The potential energy function for a particle executing linear SHM is given by `V(x) = 1/2 kx^2` where k is the force constant of the oscillator (Figure). For k = 0.5 N/m, the graph of V(x) versus x is shown in the figure. A particle of total energy E turns back when it reaches `x = ±x_m`. If V and K indicate the P.E. and K.E., respectively of the particle at `x = +x_m`, then which of the following is correct?

A block of mass m sliding on a smooth horizontal surface with a velocity \[\vec{\nu}\] meets a long horizontal spring fixed at one end and with spring constant k, as shown in following figure following. Find the maximum compression of the spring. Will the velocity of the block be the same as  \[\vec{\nu}\]  when it comes back to the original position shown?

A small block of mass 100 g is pressed against a horizontal spring fixed at one end to compress the spring through 5 cm (figure following). The spring constant is 100 N/m. When released, the block moves horizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?

When a conservative force does positive work on a body, the potential energy of the body ______.

A curved surface is shown in figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.


With the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction.

  1. For which balls is total mechanical energy conserved?
  2. Which ball (s) can reach D?
  3. For balls which do not reach D, which of the balls can reach back A?

Following figure shows a spring fixed at the bottom end of an incline of inclination 37°. A small block  of mass 2 kg starts slipping down the incline from a point 4⋅8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find (a) the friction coefficient between the plane and the block and (b) the spring constant of the spring. Take g = 10 m/s2.

One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is \[\frac{1}{2}k x^2\] . The possible cases are

(a) at spring was initially compressed by a distance x and was finally in its natural length
(b) it was initially stretched by a distance x and and finally was in its natural length
(c) it was initially in its natural length and finally in a compressed position
(d) it was initially in its natural length and finally in a stretched position.

 
Advertisements
Share
Notifications

Englishहिंदीमराठी
Login
Create free account


      Forgot password?
Course
Use app×