Displacement of an object
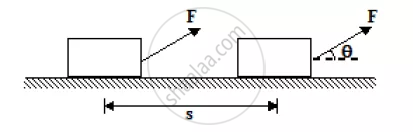
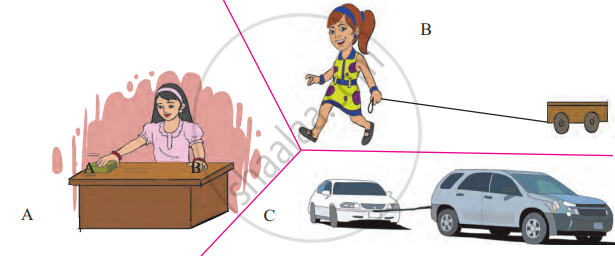
In the scenarios shown in images B and C, when a child pulls a toy with a string or a large vehicle tows a smaller one, the direction of the applied force differs from the direction of displacement. In such cases, the force is applied at an angle to the direction of movement. To calculate the work done in these situations, the applied force needs to be resolved into a component that acts along the direction of displacement.
Let F represent the applied force and F1 its component in the direction of displacement. If the displacement is s, the work done is calculated as:
W=F1⋅sHere, the force F is applied at an angle θ with respect to the horizontal direction. Using trigonometry, the horizontal component of the force (F1) can be expressed as:
F₁ = FcosθThus, the work done can be written as:
W=Fcosθ⋅sThis method allows calculating work when the force and displacement are not aligned but form an angle.
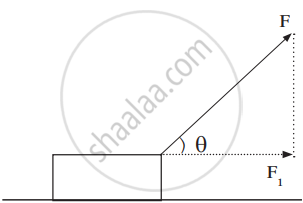
Force used for the displacement
cos θ = base / hypotenuse
cos θ = `(F_1)/(F)`
F₁ = Fcos θ
Thus, the work done by F1 is
W = F cos θ s
W = F s cos θ
Conclusions about the work done for the specific values of θ in the following table.
| θ | cos θ | W = F s cos θ | Conclusion |
|---|---|---|---|
| 0° | 1 | W = F s | Work is maximum and positive. |
| 90° | 0 | 0 | No work is done. |
| 180° | -1 | W = -F s | Work is negative. |
Unit of work:
Work = Force × Displacement
- In the SI system, the unit of force is Newton (N) and the unit of displacement is metre (m). Thus, the unit of force is the newton-meter. This is called a joule.
- 1 Joule : If a force of 1 Newton displaces an object through 1 metre in the direction of the force, the amount of work done on the object is 1 joule. 1 joule = 1 newton × 1 metre
1 J = 1 N × 1 m - In the CGS system, the unit of force is dyne and that of displacement is centimetre (cm). Thus, the unit of work done is dyne-centimetre. This is called an erg.
- 1 erg: If a force of 1 dyne displaces an object through 1 centimetre in the direction of the force, the amount of work done is 1 erg. 1 erg = 1 dyne × 1 cm
Relationship between joule and erg:
We know that 1 newton = 105 dyne and 1 m = 102 cm
Work = force × displacement
1 joule = 1 newton × 1 m
1 joule = 105 dyne× 102 cm = 107 dyne cm
1 joule = 107 erg