Work Done by a Constant Force and a Variable Force

Work Done By Friction

There is a misconception that the force of friction always does negative work. In reality, the work done by friction may be zero, positive or negative depending upon the situation.
In figure (a), when a block is pulled by a force F and the block does not move, the work done by friction is zero.
In figure (b), when a block is pulled by a force F on a stationary surface, the work done by the kinetic friction is negative.
In figure (c), block A is placed on the block B. When the block A is pulled with a force F, the friction force does negative work on block A and positive work on block B. The kinetic friction and displacement are oppositely directed in case of block A while in case of block B they are in the same direction.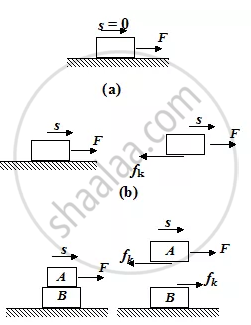

Work Done By Gravity

Consider a block of mass m which slides down a smooth inclined plane of angle θ.
Let us assume the coordinate axes as shown in the figure, to specify the components of the two vectors, although the value of work will not depend on the orientation of the axes.
Now, the force of gravity, `bar F g= −mg hat j` and the displacement is given by
`bar S = Δx hat i + Δy hat j + Δz hat k`

The work done by gravity is
`W_g = bar F_g. bar s =-mg hat j.(Δx hat i + Δ y hat j + Δz hat k)` or
`W_g =-mg Δy        ( hat j.hat i=0, hat j.hat j=1, hat j.hat k=0) `

since `Δy = y_f – y_i = -h`
`W_g = -mg (y_f - y_i) = + mgh`

If the block moves in the upward direction, then the work done by gravity is negative and is given by
Wg = - mgh

Application 3
A block of mass 10 kg is to be raised from the bottom to the top of incline 5m long and 3m off the ground at the top. Assuming frictionless surface, how much work is done by a force parallel to the incline pushing the block up at constant speed. (g = 10 m/s²)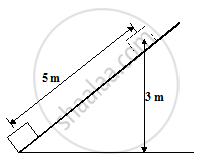

Solution:
Here, we must first find the force with which the block must be pushed. We begin by drawing a F.B.D. of the block.
Here,
F = Applied force
mg = weight of the block
N = Normal reaction by the incline on the block.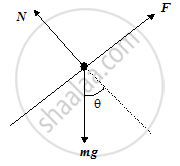

Because the motion occurs at constant speed (i.e. no acceleration), the resultant force parallel to the plane must be zero. Thus
F − mg sin θ = 0
or F = mg sin θ =10 × 1035 = 60N
Then, the work done by F is
W = F. S cos θ = 60 × 5 = 300 J.

If a person were to raise the block vertically without using the incline, the work he would do would be the vertical force mg times the vertical distance
or (10 ×10 N) × (3m) = 300 J, the same as before.
The only difference is that with the incline he could do the job with a smaller force i.e. 60 N but he has to push the block a greater distance i.e. 5 m up the incline than he had to raise the block directly (3m).
This application also illustrates the point that machines (simple or complex) can not save the amount of work that has to be done to accomplish a job, they merely allow us to do the job with less effort.

Work done by a variable force

• When the magnitude and direction of a force vary in three dimensions, it can be expressed as a function of the position vector `bar F(r)`, or in terms of the coordinates `barF (x,y,z)`.

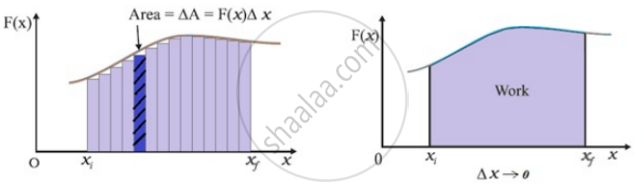
• If the displacement ds is small, we can take the force F (x) as approximately constant and the work done is then
  `dW = bar F. ds`

• The variable force is more commonly encountered than the constant force.

For total work, we add all work done along small displacements
`W = lim_(x→0) ∑_(x_i) ^(x_f) F(x)Δx `
`W =∫_(x_i)^(x_f) F(x) dx`

Example: A force F = 3 x² start acting on a particle which is initially at rest. Find the work done by the force during the displacement of the particle from x = 0 m to x = 2m.
Solution: We know that `W =∫_(x_i)^(x_f) F(x) dx`
`W =∫_0^2 3 x^2 .dx`
`W=(3(2)^3)/3-(3(0)^3)/3=8 N-m`