Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the area of the minor and major segments.
उत्तर

Let AB be the chord of a circle with centre O and radius 30 cm such that ∠AOB = 60°
Area of the sector OACBO `= (pi"r"^2theta)/360`
`=(3.14xx30xx30xx60/360)"cm"^2`
= 471 cm2
Area of ΔOAB`=1/2"r"^2"sin" theta`
`=(1/2xx30xx30xx"sin "60°)"cm"^2`
= (225 × 1.732) cm2
= 389.7 cm2
Area of the minor segment = (Area of the sector OACBO) - (Area of ΔOAB)
= (471 - 389.7) cm2
= 81.3 cm2
Area of the major segment =(Area of the circle) - (Area of minor sregment)
`=|(3.14xx30xx30) - 81.3| "cm"^2`
= 2744.7 cm2
APPEARS IN
संबंधित प्रश्न
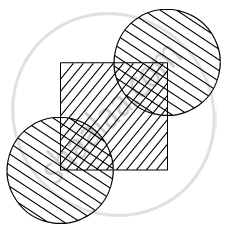
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
In a circle of radius 14 cm, an arc subtends an angle of 120° at the centre. If `sqrt(3) = 1.73` then the area of the segment of the circle is
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
The diameter of two circles are 28 cm and 24 cm. Find the circumference of the circle having its area equal to sum of the areas of the two circles.
The circumference o a garden roller is 280cm. How many revolutions does it make in moving 490m?
Circumference of a circle of diameter 5 cm is ______.
The area of a semicircle of radius 4r is ______.
