Advertisements
Advertisements
प्रश्न
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs 5 per metre sheet, sheet being 2 m wide.
उत्तर
\[\text { A closed iron tank of dimensions 12 m long, 9 m wide and 4 m deep is to be made } . \]
\[\text { Surface area of the cuboidal tank = 2 } \times\text { (length }\times \text { breadth + breadth } \times\text { height + length } \times \text { height) }\]
\[ = 2 \times (12 \times 9 + 9 \times 4 + 12 \times 4)\]
\[ = 2 \times (108 + 36 + 48)\]
\[ = 384 m^2 \]
\[\text { Also, the cost of an iron sheet is Rs 5 per metre and the sheet is 2 metres wide } . \]
\[\text { i . e . , area of a sheet = 1 m } \times 2 m = 2 m^2 \]
\[\text { So, the cost of 2 }m^2 \text { of iron sheet = Rs 5 }\]
\[\text { i . e . , the cost of 1 }m^2 \text { of iron sheet = Rs } \frac{5}{2}\]
\[ \therefore \text { Cost of 384 }m^2 \text { of iron sheet = 384 } \times \frac{5}{2} = \text { Rs } 960\]
APPEARS IN
संबंधित प्रश्न
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
The paint in a certain container is sufficient to paint on area equal to 9.375 m2. How manybricks of dimension 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
Find the volume of a cuboid whose length = 15 cm, breadth = 2.5 dm, height = 8 cm.
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 litres of milk?
How many planks each of which is 3 m long, 15 cm broad and 5 cm thick can be prepared from a wooden block 6 m long, 75 cm broad and 45 cm thick?
A cuboidal box is 5 cm by 5 cm by 4 cm. Find its surface area.
The volume of a cuboid is 3456 cm3. If its length = 24 cm and breadth = 18 cm ; find its height.
The dimension of a class-room are; length = 15 m, breadth = 12 m and height = 7.5 m. Find, how many children can be accommodated in this class-room; assuming 3.6 m3 of air is needed for each child.
Find the Total Surface Area and the Lateral Surface Area of a cuboid whose dimensions are: length = 20 cm, breadth = 15 cm, height = 8 cm
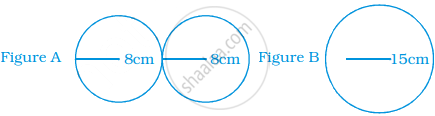
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?