Advertisements
Advertisements
प्रश्न
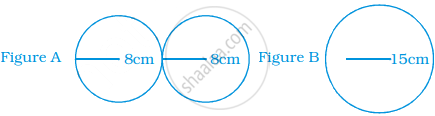
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?
उत्तर
In figure A, 2 pipes each having a radius of 8 cm
∵ Area of a circle = πr2
∴ Area of one pipe = `22/7 xx 8 xx 8`
= `(22 xx 8 xx 8)/7`
= `(22 xx 64)/7` cm2
Area of 2 pipes = `(2 xx 1408)/7`
= `2816/7` cm2
= 402.28 cm2
In figure B, a pipe having radius of 15 cm
∴ Area of the pipe = πr2
= `22/7 xx 15 xx 15`
= `22/7 xx 225`
= `4950/7`
= 707.14 cm2
Clearly, the surface area of pipe B is greater. So, pipe B fills the swimming pool faster.
APPEARS IN
संबंधित प्रश्न
Find the volume of a cuboid whose length =1.2 m, breadth = 30 cm, height = 15 cm.
Find the volume of a cuboid whose length = 15 cm, breadth = 2.5 dm, height = 8 cm.
What will happen to the volume of a cuboid if its Length is doubled, height is doubled and breadth is sama?
An 8 m long cuboidal beam of wood when sliced produces four thousand 1 cm cubes and there is no wastage of wood in this process. If one edge of the beam is 0.5 m, find the third edge.
The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at Rs 3.50 per square metre.
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the wall.
The curved surface area and the volume of a toy, cylindrical in shape, are 132 cm2 and 462 cm3 respectively. Find, its diameter and its length.
A matchbox is 4 cm long, 2.5 cm broad, and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?
The total surface area of a cuboid with dimension 10 cm × 6 cm × 5 cm is
External dimensions of a closed wooden box are in the ratio 5:4:3. If the cost of painting its outer surface at the rate of Rs 5 per dm2 is Rs 11,750, find the dimensions of the box.
