Advertisements
Advertisements
Question
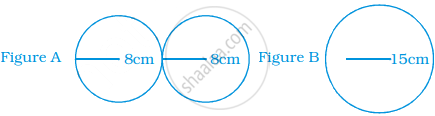
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?
Solution
In figure A, 2 pipes each having a radius of 8 cm
∵ Area of a circle = πr2
∴ Area of one pipe = `22/7 xx 8 xx 8`
= `(22 xx 8 xx 8)/7`
= `(22 xx 64)/7` cm2
Area of 2 pipes = `(2 xx 1408)/7`
= `2816/7` cm2
= 402.28 cm2
In figure B, a pipe having radius of 15 cm
∴ Area of the pipe = πr2
= `22/7 xx 15 xx 15`
= `22/7 xx 225`
= `4950/7`
= 707.14 cm2
Clearly, the surface area of pipe B is greater. So, pipe B fills the swimming pool faster.
APPEARS IN
RELATED QUESTIONS
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
 |
 |
| (a) | (b) |
The volume of a cuboidal box is 48 cm3. If its height and length are 3 cm and 4 cm respectively, find its breadth.
Find the surface area of a cuboid whoselength = 3.2 m, breadth = 30 dm, height = 250 cm.
A cuboid has total surface area of 50 m2 and lateral surface area is 30 m2. Find the area of its base.
If two cubes each of side 6 cm are joined face to face, then find the volume of the resulting cuboid.
If the sum of all the edges of a cube is 36 cm, then the volume (in cm3) of that cube is
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is ` 5 sqrt(5)` cm. Its surface area is
If A1, A2, and A3 denote the areas of three adjacent faces of a cuboid, then its volume is
The volume of a cuboid is 3456 cm3. If its length = 24 cm and breadth = 18 cm ; find its height.
The total surface area of a cuboid is 46m2. If its height is 1m and breadth 3m, find its length and volume.
