Advertisements
Advertisements
Question
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is ` 5 sqrt(5)` cm. Its surface area is
Options
361 cm2
125 cm2
236 cm2
486 cm2
Solution
Let,
l → Length of the cuboid
b → Breadth of the cuboid
h → Height of the cuboid
We have,
l + b + h = 19 cm , diagonal of the cuboid
`( sqrt(l^2 + b^2 +h^2)) = 5 sqrt(5) cm `
We are asked to find the surface area
So, the surface area,
= 2 (lb + bh + hl )
= (l + b +h )2 - ( l2 + b2 + h2 )
`=(l + b+ h) - ( sqrt (l^2 + b^2 + h^2 ))^2`
`=19^2 - (5sqrt(5))^2`
=361-125
=236 cm2
Thus, the surface area is 236 cm2
APPEARS IN
RELATED QUESTIONS
Ravish wanted to make a temporary shelter for his car by making a box-like structure with tarpaulin that covers all the four sides and the top of the car ( with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m with
base dimensions 4 m × 3m?
An ice-cream brick measures 20 cm by 10 cm by 7 cm. How many such bricks can be stored in deep fridge whose inner dimensions are 100 cm by 50 cm by 42 cm?
Show that the product of the areas of the floor and two adjacent walls of a cuboid is the square of its volume.
Three equal cubes are placed adjacently in a row. The ratio of the total surface area of the resulting cuboid to that of the sum of the surface areas of three cubes, is
If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then `A/V`
The volume of a cuboid is 7.68 m3. If its length = 3.2 m and height = 1.0 m; find its breadth.
In a building, there are 24 cylindrical pillars. For each pillar, the radius is 28 m, and the height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m2.
A matchbox is 4 cm long, 2.5 cm broad, and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?
The length breadth and height of a cuboid are in the ratio of 3 : 3 : 4. Find its volume in m3 if its diagonal is `5sqrt(34)"cm"`.
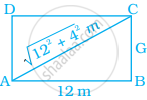
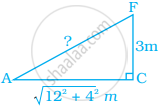
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.