Advertisements
Advertisements
प्रश्न
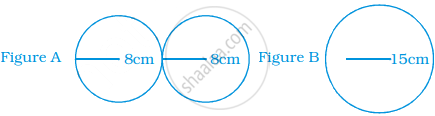
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?
उत्तर
In figure A, 2 pipes each having a radius of 8 cm
∵ Area of a circle = πr2
∴ Area of one pipe = `22/7 xx 8 xx 8`
= `(22 xx 8 xx 8)/7`
= `(22 xx 64)/7` cm2
Area of 2 pipes = `(2 xx 1408)/7`
= `2816/7` cm2
= 402.28 cm2
In figure B, a pipe having radius of 15 cm
∴ Area of the pipe = πr2
= `22/7 xx 15 xx 15`
= `22/7 xx 225`
= `4950/7`
= 707.14 cm2
Clearly, the surface area of pipe B is greater. So, pipe B fills the swimming pool faster.
APPEARS IN
संबंधित प्रश्न
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
 |
 |
| (a) | (b) |
The paint in a certain container is sufficient to paint on area equal to 9.375 m2. How manybricks of dimension 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
The dimensions of a cuboid are in the ratio 5 : 3 : 1 and its total surface area is 414 m2. Find the dimensions.
The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5 m, 3 m and 350 cm, respectively. Find the cost of plastering at the rate of Rs 8 per square metre.
If each edge of a cuboid of surface area S is doubled, then surface area of the new cuboid is
Volume of a cuboid is 12 cm3. The volume (in cm3) of a cuboid whose sides are double of the above cuboid is
If A1, A2, and A3 denote the areas of three adjacent faces of a cuboid, then its volume is
A closed rectangular box is made of wood of 1.5 cm thickness. The exterior length and breadth are respectively 78 cm and 19 cm, and the capacity of the box is 15 cubic decimeters. Calculate the exterior height of the box.
Opposite faces of a cuboid are ______ in area.
