Advertisements
Advertisements
Question
The volume of a cuboidal box is 48 cm3. If its height and length are 3 cm and 4 cm respectively, find its breadth.
Solution
\[\text { Suppose that the breadth of the box is b cm }. \]
\[\text { Volume of the cuboidal box = 48 } {cm}^3 \]
\[\text { Height of the box }= 3 cm \]
\[\text { Length of the box }= 4 cm\]
\[\text { Now, volume of box = length }\times \text { breadth } \times \text { height }\]
\[ \Rightarrow 48 = 4 \times b \times 3\]
\[ \Rightarrow 48 = 12 \times b\]
\[ \Rightarrow b = \frac{48}{12} = 4 cm\]
\[ \therefore \text { The breadth of the cuboidal box is 4 cm } .\]
APPEARS IN
RELATED QUESTIONS
The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1 .2 m and each window 1 .5 m by I m. Find the cost of painting the walls at Rs. 3.50 per square metre.
A tank is 8 m long, 6 m broad and 2 m high. How much water can it contain?
A swimming pool is 250 m long and 130 m wide. 3250 cubic metres of water is pumped into it. Find the rise in the level of water.
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
The number of cubes of side 3 cm that can be cut from a cuboid of dimensions 10 cm × 9 cm × 6 cm, is ______.
The length, breadth, and height of a cuboid are in the ratio 6: 5 : 3. If its total surface area is 504 cm2; find its dimensions. Also, find the volume of the cuboid.
The total surface area of a cube is 216 cm2. Find its volume.
A closed box measures 66 cm, 36 cm and 21 cm from outside. If its walls are made of metal-sheet, 0.5 cm thick; find :
(i) the capacity of the box ;
(ii) the volume of metal-sheet and
(iii) weight of the box, if 1 cm3 of metal weighs 3.6 gm.
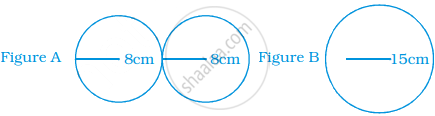
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?