Advertisements
Advertisements
प्रश्न
A convex lens of focal length 25 cm and a concave lens of focal length 10 cm are placed in close contact with one another.
(a) What is the power of this combination?
(b) What is the focal length of this combination?
(c) Is this combination converging or diverging?
उत्तर
Focal length of convex lens f1 = + 25 cm = + 0.25 m
Power of convex lens`p_1=1/(f_1)=1/0.25=4D`
Focal length of concave lens f2 = - 10 cm = - 0.10 m
Power of concave lens `p_2=1/(f_2)=1/-0.10=-10D`
(a) The power of the combination of lenses is the algebraic sum of the powers of the individual lenses.
∴ Power of combination P = P1 + P2
⇒ P = 4 - 10 = - 6 D.
(b) Suppose, the focal length of the combination of the lenses is f.
The power of a lens and the focal length are related as:
`p=1/f`
`-6=1/f`
`f=1/-6=-0.167m -16.7 cm`
Therefore, the focal length of the combination of the lenses is - 16.7 cm.
(c) The focal length of the combination of the lenses is - 16.7 cm. Here, the negative sign shows that the combination of the two lenses acts like a concave lens. Therefore, this combination of lenses is diverging.
APPEARS IN
संबंधित प्रश्न
Calculate the focal length of a corrective lens having power +2D.
How unit of power related to focal length of a lens?
Which of the two has a greater power: a lens of short focal length or a lens of large focal length?
What is the unit of power of a lens? Define the unit of power of a lens.
Define power of a lens. Write its units. Deduce the relation `1/f =1/f_1 +1/f_2`for two thin lenses kept in contact coaxially.
A symmetric double convex lens in cut in two equal parts by a plane perpendicular to the principal axis. If the power of the original lens was 4 D, the power a cut-lens will be
Consider three converging lenses L1, L2 and L3 having identical geometrical construction. The index of refraction of L1 and L2 are \[\mu_1 \text{ and } \mu_2\] respectively. The upper half of the lens L3 has a refractive index \[\mu_1\] and the lower half has \[\mu_2\] following figure . A point object O is imaged at O1 by the lens L1 and at O2 by the lens L2placed in same position. If L3 is placed at the same place,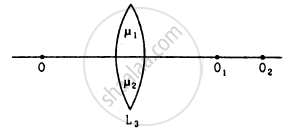
(a) there will be an image at O1
(b) there will be an image at O2.
(c) the only image will form somewhere between O1 and O2
(d) the only image will form away from O2.
A pin of length 2.00 cm is placed perpendicular to the principal axis of a converging lens. An inverted image of size 1.00 cm is formed at a distance of 40.0 cm from the pin. Find the focal length of the lens and its distance from the pin.
If the lens is of focal length 25 cm. Calculate the power of the lens.
The lens of power + 1·0 D is ______.
