Advertisements
Advertisements
प्रश्न
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.
उत्तर
We have,
base radius of the cylinder, r = 8 cm,
Height of the cylinder, h = 2 cm and
Height of the cone, H = 6 cm
Let the base radius of the cone be R.
`=> 1/3 pi"R"^2"H" = pi"r"^2"h"`
`=> "R"^2 = ("3r"^2"h")/"H"`
`=> "R"^2 = (3xx8xx8xx2)/6`
`=> "R"^2 = 64`
`=> "R" = sqrt(64)`
∴ R = 8 cm
So, the radius of the base of the cone is 8 cm.
APPEARS IN
संबंधित प्रश्न
A spherical ball of radius 3cm is melted and recast into three spherical balls. The radii of the two of balls are 1.5cm and 2cm . Determine the diameter of the third ball?
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
A boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
A metallic cone of radius 12 cm and height 24 cm is melted and made into spheres of radius 2 cm each. How many spheres are formed?
Choose the correct answer of the following question:
If the radius of a sphere becomes 3 times, then its volume will become
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its : curved surface area.
In the given figure, AB is the diameter of a circle with center O and OA = 7 cm. Find the area of the shaded region.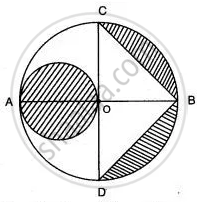
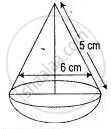
The given figure represents a hemisphere surmounted by a conical block of wood. The diameter of their bases is 6 cm each and the slant height of the cone is 5 cm. Calculate:
(i) the height of the cone.
(ii) the vol. of the solid.
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that `1/8` space is covered by the mortar. Then the number of bricks used to construct the wall is ______.
