Advertisements
Advertisements
प्रश्न
A disc of radius R is rotating with an angular speed ωo about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is µk.
- What was the velocity of its centre of mass before being brought in contact with the table?
- What happens to the linear velocity of a point on its rim when placed in contact with the table?
- What happens to the linear speed of the centre of mass when disc is placed in contact with the table?
- Which force is responsible for the effects in (b) and (c).
- What condition should be satisfied for rolling to begin?
- Calculate the time taken for the rolling to begin.
उत्तर
a. Before being brought in contact with the table the disc was in pure rotational motion hence, vCM = 0.
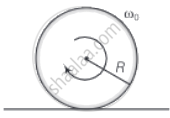
b. When the disc is placed in contact with the table due to friction velocity of a point on the rim decreases.
c. When the rotating disc is placed in contact with the table due to friction centre of mass acquires some linear velocity.
d. Friction is responsible for the effects in (b) and (c) .
e. When rolling starts vCM = ωR.
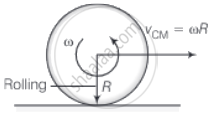
Where ω is the angular speed of the disc when rolling just starts.
f. Acceleration produced in the centre of mass due to friction
aCM = `F/M - (μ_k mg)/m = μ_k g`

Angular retardation is produced by the torque due to friction.
α = `τ/I = (μ_k mgR)/I` ......[∵ τ = (μkN)R = μkmgR]
∴ vCM = uCM + aCMt
⇒ vCM = μkgt ......(∵ uCM = 0)
And ω = ω0 + αt
⇒ `ω = ω_0 - (μ_k mgR)/I t`
For rolling without slipping, `v_(CM)/R` = ω
⇒ `v_(CM)/R = ω_0 - (μ_k mgR)/I t`
`(μ_k g t)/R = ω_0 - (μ_k mgR)/I t`
t = `(Rω_0)/(μ_kg(1 + (mR^2)/I))`
APPEARS IN
संबंधित प्रश्न
The motion of the centre of mass depends on
For a system of particles and rigid body,
A wheel in uniform motion about an axis passing through its centre and perpendicular to its plane is considered to be in mechanical (translational plus rotational) equilibrium because no net external force or torque is required to sustain its motion. However, the particles that constitute the wheel do experience a centripetal acceleration directed towards the centre. How do you reconcile this fact with the wheel being in equilibrium? How would you set a half-wheel into uniform motion about an axis passing through the centre of mass of the wheel and perpendicular to its plane? Will you require external forces to sustain the motion?
