Advertisements
Advertisements
प्रश्न
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
उत्तर
a. As there is no net external torque on the system, the law of conservation of angular momentum may be applied.
Gravitational forces and their normal reactions are external forces, but their net torque is zero, therefore they have no impact.
b. By applying the Law of conversation of angular momentum,
`L_j = L_i`
⇒ `I_ω = I_1ω_1 + I_2ω_2`
I = moment of inertia
ω = angular speed
∴ ω = `(I_1ω_1 + ω_2ω_2)/I` ∴ I = I1 + I2
∴ ω = `(I_1ω_1 + ω_2ω_2)/I`
c. As `KE_f = KE_R + KE_T`
Translational Energy = 0
∴ KET = 0
∴ `KE_f = KE_R = 1/2 Iω^2 = 1/2 (I_1 + I_2) [(I_1ω_1 + I_2ω_2)/(I_1 + I_2)]^2`
`KE_f = 1/2 (I_1ω_1 + I_2ω_2)^2/((I_1 + I_2))`
`KE_i = KE_(1R) + KE_(2R) + KE_(1T) + KE_(2T)`
Because there is no translational motion which in turn results,
KE1T = 0
KE2T = 0
∴ `KE_i = 1/2 I_1ω_1^2 + 1/2 I_2ω_2^2 = 1/2 (I_1ω_1^2 + I_2ω_2^2)`
∴ `ΔKE = KE_f - KE_i = 1/2 (I_1ω_1 + I_2ω_2)^2/((I_1 + I_2)) - 1/2 (I_1ω_1^2 + I_2ω_2^2)`
= `1/2 [(I_1^2ω_1^2 + I_2^2ω_2^2 + 2I_1I_2ω_1ω_2 - [(I_1 + I_2)(I_1ω_1^2 + I_2w_2^2)]]/(I_1 + I_2)]`
= `[([I_1^2ω_1^2 + I_2^2ω_2^2 + 2I_1I_2ω_1ω_2] - [I_1^2ω_1^2 + I_2^2ω_2^2 + I_1I_2ω_1^2 + I_2^2ω_2^2])/(2(I_1 + I_2))]`
= `(-I_1I_2)/(2(I_1 + I_2)) (-2ω_1ω_2 + ω_2^2 + ω_1^2)`
ΔKE = `(-I_1I_2)/(2(I_1 + I_2)) (ω_1 - ω_2)^2 < 0`
d. `K_f < K_i` since energy is wasted due to friction between discs' moving surfaces.
APPEARS IN
संबंधित प्रश्न
The torque of a force \[\overrightarrow F \] about a point is defined as \[\overrightarrow\Gamma = \overrightarrow r \times \overrightarrow F.\] Suppose \[\overrightarrow r, \overrightarrow F\] and \[\overrightarrow \Gamma\] are all nonzero. Is \[r \times \overrightarrow\Gamma || \overrightarrow F\] always true? Is it ever true?
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
A 6⋅5 m long ladder rests against a vertical wall reaching a height of 6⋅0 m. A 60 kg man stands half way up the ladder.
- Find the torque of the force exerted by the man on the ladder about the upper end of the ladder.
- Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
Define torque and mention its unit.
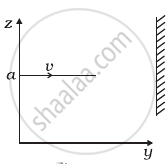
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
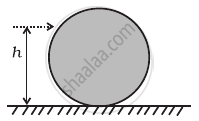
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
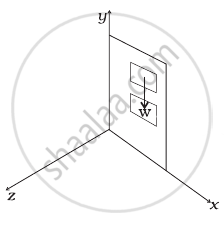
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
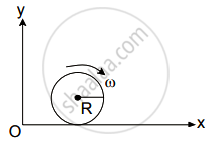
Angular momentum of a single particle moving with constant speed along the circular path ______.
