Advertisements
Advertisements
प्रश्न
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
पर्याय
2ω
ω
`ω/2`
0
उत्तर
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is 2ω.
Explanation:
`I_1ω_1 = I_2ω_2`
`m_1 = 2M`
`m_2 = M`
`ω_1 = ω`
`ω_2` = ?
`r_1 = R`
`r_2 = R`
When a person leaps down tangentially, i.e. from the perimeter,
∴ `m_1r_1^2ω_1 = m_2r_2^2ω_2`
`2MR^2ω = MR^2ω_2`
`ω_2 = 2ω`
APPEARS IN
संबंधित प्रश्न
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
A body is in translational equilibrium under the action of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
A simple pendulum of length l is pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weight ω of the bob about the point of suspension. When is the torque zero?
A flywheel of moment of inertia 5⋅0 kg-m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle it comes to rest in 5⋅0 minutes. Find (a) the average torque of the friction (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
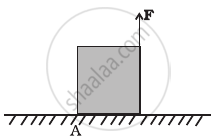
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
The position vector of 1 kg object is `vecr = (3hati - hatj)` m and its velocity `vecv = (3hati + hatk)` ms-1. The magnitude of its angular momentum is `sqrtx` Nm where x is ______.
