Advertisements
Advertisements
प्रश्न
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
उत्तर
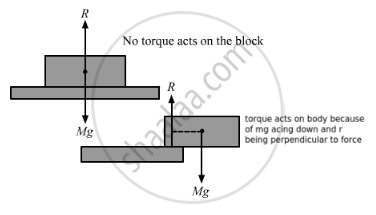
The centre of mass (CM) of a rectangular block lies in the middle of the block . When the block is projected less than half of its length (CM being over the table), no net force acts on it . Thus, no net torque acts upon the body . But if the block is projected more than half of its length outside the table (CM being outside the table), gravitational force acts along the CM of the block . This force produces a moment along the edge of the table . This rotates the block, and as a result, it falls down.
APPEARS IN
संबंधित प्रश्न
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
A heavy particle of mass m falls freely near the earth's surface. What is the torque acting on this particle about a point 50 cm east to the line of motion? Does this torque produce any angular acceleration in the particle?
If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?
Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are \[\nu_A\] and \[\nu_B\] respectively. We have
The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis though the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are ________________ .
A simple pendulum of length l is pulled aside to make an angle θ with the vertical. Find the magnitude of the torque of the weight ω of the bob about the point of suspension. When is the torque zero?
Calculate the total torque acting on the body shown in the following figure about the point O.

A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N?
Define torque and mention its unit.
What are the conditions in which force can not produce torque?
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed v along parallel lines. At a particular instant, r1 and r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options:
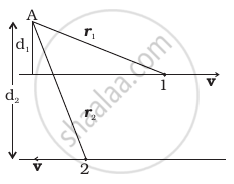
- Angular momentum l1 of particle 1 about A is l1 = mvd1
- Angular momentum l2 of particle 2 about A is l2 = mvr2
- Total angular momentum of the system about A is l = mv(r1 + r2)
- Total angular momentum of the system about A is l = mv (d2 − d1)
⊗ represents a unit vector coming out of the page.
⊗ represents a unit vector going into the page.
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
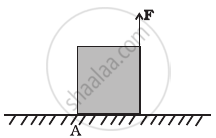
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
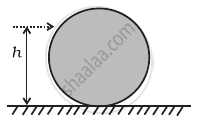
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
A solid sphere is rotating in free space. If the radius of the sphere is increased while keeping the mass the same, which one of the following will not be affected?
