Advertisements
Advertisements
प्रश्न
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
उत्तर
| Column I | Column II | |
| (a) h = R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (b) h = R | (iv) | Sphere has only a translational motion, looses energy by friction. |
| (c) h = 3R/2 | (ii) | Sphere spins clockwise, loses energy by friction. |
| (d) h = 7R/5 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
Explanation:
Mass of the sphere = m
Radius = R
h = height from the floor
The sphere will roll without slipping when ω = V/R
Where v is linear velocity and to is the angular velocity of the sphere.
Now, angular momentum of the sphere is about centre of mass .....[We are applying conservation of angular momentum just before and after struck.]
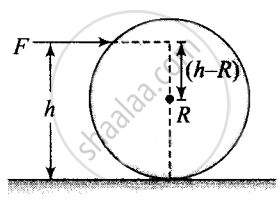
Then by the law of conservation of angular momentum
`mv(h - R) = I_ω`
`mv(h - R) = 2/5 mR^2 v/R`
`h - R = 2/5 R`
`h = 2/5 R +R = 7/5 R`
Therefore, the sphere rolls without slipping with a constant velocity and no loss of energy. Thus (d) - (i)
Torque due to force `F = τ = (h - R) xx F`
If τ = 0, h – R = 0 and thus h = R
In this case, the sphere will only have a translation motion and slip against the force of friction. Thus (b) - (iv)
For clockwise rotation of the sphere τ > 0
`(h - R) xx F > 0`
Or `h > R`, thus (c) - (ii)
For anti-clockwise rotation `τ < 0`
`(h - R) xx F < 0`
`h < R`,Thus (a) - (iii)
APPEARS IN
संबंधित प्रश्न
A body is in translational equilibrium under the action of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?
A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. If it more likely to slip when a man stands near the bottom or near the top?
When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?
Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are \[\nu_A\] and \[\nu_B\] respectively. We have
A 6⋅5 m long ladder rests against a vertical wall reaching a height of 6⋅0 m. A 60 kg man stands half way up the ladder.
- Find the torque of the force exerted by the man on the ladder about the upper end of the ladder.
- Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
A particle is moving with a constant velocity along a line parallel to the positive X-axis. The magnitude of its angular momentum with respect to the origin is, ______
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is, ______
A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is ______.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω2 and ω2 are brought into contact face to face with their axes of rotation coincident.
- Does the law of conservation of angular momentum apply to the situation? why?
- Find the angular speed of the two-disc system.
- Calculate the loss in kinetic energy of the system in the process.
- Account for this loss.
The magnitude of the torque on a particle of mass 1 kg is 2.5 Nm about the origin. If the force acting on it is 1 N, and the distance of the particle from the origin is 5 m, the angle between the force and the position vector is (in radians) ______.
