Advertisements
Advertisements
प्रश्न
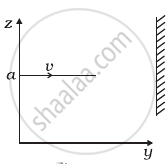
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is ______.
पर्याय
`mva hate_x`
`2mva hate_x`
`ymv hate_x`
`2ymv hate_x`
उत्तर
A particle of mass m is moving in yz-plane with a uniform velocity v with its trajectory running parallel to + ve y-axis and intersecting z-axis at z = a (Figure). The change in its angular momentum about the origin as it bounces elastically from a wall at y = constant is `underline(2mva hate_x)`.
Explanation:
The initial velocity is `vhati = vhate_y` and, after reflection from the wall, the final velocity is `v_f = - vhate_y`. The trajectory is described as `r = yhate_y + ahate_z`. Hence the change in angular momentum is `r xx m(v_f - v_i) = 2mvahate_x`.
APPEARS IN
संबंधित प्रश्न
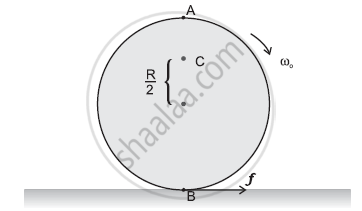
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
The torque of the weight of any body about any vertical axis is zero. If it always correct?
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
A body is in translational equilibrium under the action of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?
When a force of 6⋅0 N is exerted at 30° to a wrench at a distance of 8 cm from the nut it is just able to loosen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Figure). The sphere is struck horizontally at a height h from the floor. Match the following:
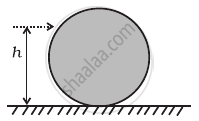
| Column I | Column II | |
| (a) h = R/2 | (i) | Sphere rolls without slipping with a constant velocity and no loss of energy. |
| (b) h = R | (ii) | Sphere spins clockwise, loses energy by friction. |
| (c) h = 3R/2 | (iii) | Sphere spins anti-clockwise, loses energy by friction. |
| (d) h = 7R/5 | (iv) | Sphere has only a translational motion, looses energy by friction. |
A door is hinged at one end and is free to rotate about a vertical axis (Figure). Does its weight cause any torque about this axis? Give reason for your answer.
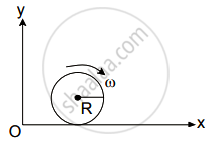
A spherical shell of 1 kg mass and radius R is rolling with angular speed ω on horizontal plane (as shown in figure). The magnitude of angular momentum of the shell about the origin O is `a/3 R^2` ω. The value of a will be:
Angular momentum of a single particle moving with constant speed along the circular path ______.
